Question

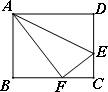
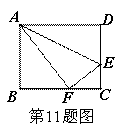
已知矩形的周长是72cm，一边中点与对边的两个端点连线的夹角为直角，则此矩形的长边和短边长分别是

1. A.
   26cm　 10cm
2. B.
   25cm　11cm
3. C.
   24cm　12cm
4. D.
   23cm　13cm

Answer 1

C
分析：作出图形，根据矩形的对边相等，四个角都是直角，利用“边角边”证明△ABE和△DCE全等，根据全等三角形对应边相等可得BE=CE，从而得到△BCE是等腰直角三角形，然后求出△ABE与△CDE都是等腰直角三角形，从而得到矩形的短边等于长边的一半，然后根据矩形的周长进行计算即可得解．
解答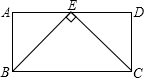：解：如图，∵E是AD的中点，
∴AE=DE，
在△ABE和△DCE中，，
∴△ABE≌△DCE（SAS），
∴BE=CE，
∵BE⊥CE，
∴△BCE是等腰直角三角形，
∴∠EBC=∠ECB=45°，
∴∠ABE=∠DCE=90°-45°=45°，
∴△ABE与△CDE都是等腰直角三角形，
∴AB=AE=AD，
∴2（AB+AD）=2（AD+AD）=3AD=72，
解得AD=24cm，
AB=×24=12cm，
即，此矩形的长边和短边长分别是24cm，12cm．
故选C．
点评：本题考查了矩形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，求出矩形的短边等于长边的一半是解题的关键．