题目内容
泖塔是青浦沈巷泖河中小岛上的一座古塔,建于唐乾符年间(874-879年),是五级四面的方形塔砖.某校数学兴趣小组要测量的古塔的高度.如图,他们在C处测得古塔的最高点A的仰角为30°,再往古塔的方向前进18cm至D处,测得最高点A的仰角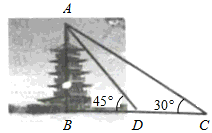 为45°(点B、D、C在一条直线上).求该兴趣小组测得的泖塔高度AB.(结果保留根号)
为45°(点B、D、C在一条直线上).求该兴趣小组测得的泖塔高度AB.(结果保留根号)
解:根据题意可知:∠BDA=45°,∠BCA=30°,DC=18m,
在Rt△ABD中,由∠BAD=∠BDA=45°,得AB=BD,
在Rt△BCA中,由tan∠BCA=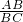 得,AB=BCtan30°=
得,AB=BCtan30°= BC,
BC,
∴BC= AB
AB
又∵BC-BD=DC,
∴ AB-AB=18,
AB-AB=18,
∴AB=9 +9.
+9.
答:该古塔的高度约为(9 +9)米.
+9)米.
分析:先根据题意得出:∠BDA、∠BCA的度数及AC的长,再在Rt△ABD中可得出AB=BD,利用锐角三角函数的定义可得出BA的长.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,涉及到等腰直角三角形的判定与性质、锐角三角函数的定义及特殊角的三角函数值,熟练掌握以上知识是解答此题的关键.
在Rt△ABD中,由∠BAD=∠BDA=45°,得AB=BD,
在Rt△BCA中,由tan∠BCA=
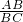 得,AB=BCtan30°=
得,AB=BCtan30°= BC,
BC,∴BC=
 AB
AB又∵BC-BD=DC,
∴
 AB-AB=18,
AB-AB=18,∴AB=9
 +9.
+9.答:该古塔的高度约为(9
 +9)米.
+9)米.分析:先根据题意得出:∠BDA、∠BCA的度数及AC的长,再在Rt△ABD中可得出AB=BD,利用锐角三角函数的定义可得出BA的长.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,涉及到等腰直角三角形的判定与性质、锐角三角函数的定义及特殊角的三角函数值,熟练掌握以上知识是解答此题的关键.

练习册系列答案
相关题目
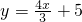 的图象与x轴交于A点,
的图象与x轴交于A点,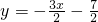 的图象与y轴交于B点,这两个一次函数的图象相交于P点,则△ABP的面积是________.
的图象与y轴交于B点,这两个一次函数的图象相交于P点,则△ABP的面积是________.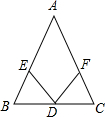 如图,在△ABC中,如果AB=AC,且EB=BD=DC=CF,∠A=44°,那么∠EDF的度数是
如图,在△ABC中,如果AB=AC,且EB=BD=DC=CF,∠A=44°,那么∠EDF的度数是 )-1的结果是
)-1的结果是
 如图,C为线段AB上一点,在AB的同侧作等边△ACM和等边△BCN,连接AN、BM,若∠MBN=40°,则∠ANB的大小是
如图,C为线段AB上一点,在AB的同侧作等边△ACM和等边△BCN,连接AN、BM,若∠MBN=40°,则∠ANB的大小是 如图,在等腰△ABC中,∠A=36°,BD平分∠B交AC于点D,则∠BDC等于
如图,在等腰△ABC中,∠A=36°,BD平分∠B交AC于点D,则∠BDC等于