题目内容
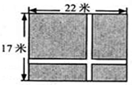
如图,在一块长为22m、宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形一边平行),剩余部分种上草坪,使草坪面积为300m2.若设道路宽为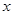 m,则根据题意可列方程为 __ .
m,则根据题意可列方程为 __ .
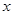 m,则根据题意可列方程为 __ .
m,则根据题意可列方程为 __ .
(22-x)(17-x)=300或者22×17-22x-17x+x2=300.
方法一:矩形的总面积是22×17 m2,横道路面积是22x m2,竖道路面积是17x m2,横竖道路重合面积x2 m2,由题草坪面积是300m2,可列方程22×17-22x-17x+x2=300;
方法二:将两条道路分别移到一角,可得草坪的长是(22-x)m,宽是(17-x)m,由题草坪面积是300m2,可列方程(22-x)(17-x)=300.
试题分析:通常的想法是用总的面积减去道路的面积,剩下的是草坪的面积,矩形的面积是22×17 m2,道路的面积有一部分重合,重合部分的面积是x2 m2,横道路面积是22x m2,竖道路面积是17x m2,而草坪面积是300m2,可列方程22×17-22x-17x+x2=300;也可以将两条道路分别移到一角,此时草坪是一个矩形,可得草坪的长是(22-x)m,宽是(17-x)m,由题草坪面积是300m2,可列方程(22-x)(17-x)=300.
方法二:将两条道路分别移到一角,可得草坪的长是(22-x)m,宽是(17-x)m,由题草坪面积是300m2,可列方程(22-x)(17-x)=300.
试题分析:通常的想法是用总的面积减去道路的面积,剩下的是草坪的面积,矩形的面积是22×17 m2,道路的面积有一部分重合,重合部分的面积是x2 m2,横道路面积是22x m2,竖道路面积是17x m2,而草坪面积是300m2,可列方程22×17-22x-17x+x2=300;也可以将两条道路分别移到一角,此时草坪是一个矩形,可得草坪的长是(22-x)m,宽是(17-x)m,由题草坪面积是300m2,可列方程(22-x)(17-x)=300.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程 .
. 取哪些整数时,x1、x2均为整数;
取哪些整数时,x1、x2均为整数; ,求k的值.
,求k的值.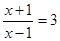 解相同.
解相同. ; (2)
; (2)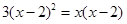 ;
;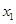 、
、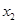 是一元二次方程x2+5x+4=0的两个根,则
是一元二次方程x2+5x+4=0的两个根,则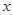 ,则根据题意可列出方程: .
,则根据题意可列出方程: . 的一个根,则a= .
的一个根,则a= .