Question

【题目】如图，已知直线l1∥l2 ， 直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．

（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？

Answer 1

【答案】
（1）解：当点P在C、D之间运动时,∠APB=∠PAC+∠PBD．理由如下：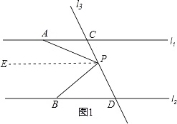
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD；
（2）解：ⅰ）当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB．理由如下：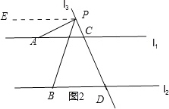
过点P作PE∥l1
∴∠EPA=∠PAC,
∵l1∥l2,PE∥l1
∴PE∥l2
∴∠EPB=∠PBD,
∵∠EPB=∠EPA＋∠APB =∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB．
ⅱ）当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB．理由如下：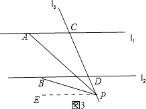
过点P作PE∥l2;
∴∠DBP=∠BPE;
∵l1∥l2,PE∥l2;
∴PE∥l1
∴∠EPA=∠PAC,
∵∠EPA=∠EPB＋∠BPA=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB．
【解析】(1)当点P在C、D之间运动时,∠APB=∠PAC+∠PBD．理由如下： 过点P作PE∥l1,根据平行于同一直线的两条直线互相平行得出PE∥l2∥l1,根据二直线平行内错角相等得出∠PAC=∠1,∠PBD=∠2,根据角的和差及等量代换得出∠APB=∠1+∠2=∠PAC+∠PBD；
（2）①当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB．理由如下： 过点P作PE∥l1根据二直线平行，内错角相等得出 ∠EPA=∠PAC, 根据平行于同一条直线的两条直线互相平行得出 PE∥l2，根据二直线平行内错角相等得出∠EPB=∠PBD, ,根据角的和差，及等量代换得出 ∠EPB=∠EPA＋∠APB =∠PAC+∠APB, 从而得出结论∠PBD=∠PAC+∠APB；②当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB．理由如下： 过点P作PE∥l2; 根据二直线平行，内错角相等得出∠DBP=∠BPE;根据平行于同一条直线的两条直线互相平行得出PE∥l1，根据二直线平行内错角相等得出∠EPA=∠PAC,根据角的和差，及等量代换得出∠EPA=∠EPB＋∠BPA=∠PBD+∠APB,从而得出结论∠PAC=∠PBD+∠APB．
【考点精析】本题主要考查了平行线的判定与性质的相关知识点，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质才能正确解答此题．