题目内容
（2011贵州六盘水，23，14分）如图8，已知：△ABC是⊙O的内接三角形，D是OA延
长线上的一点，连接DC，且∠B＝∠D＝300。
（1）判断直线CD与⊙O的位置关系，并说明理由。
（2）若AC=6，求图中弓形（即阴影部分）的面积。
解：（1）直线CD是⊙O的切线
理由如下：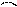
连接OC
∵∠AOC、∠ABC分别是AC所对的圆心角、圆周角
∴∠AOC＝2∠ABC＝2×300＝600
∴∠D＋∠AOC＝300＋600＝900
∴∠DCO＝900
∴CD是⊙O的切
线
（2）过O作OE⊥AC，点E为垂足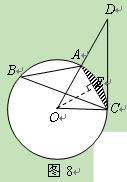
∵OA＝OC，∠ AOC＝600
∴△AOC是等边三角形
∴OA＝OC＝AC＝6，∠OAC＝600
在Rt△AOE中
OE＝OA·sin∠OAC＝6·sin600＝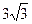
∴
∵
∴
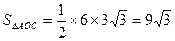
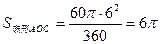
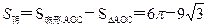
解析
练习册系列答案
相关题目
、
）
