题目内容
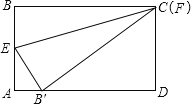
【题目】如图,折叠矩形纸片ABCD,使点B落在边AD上,折叠EF的两端分别在AB、BC上(含端点),且AB=8cm,BC=10cm,则折痕EF的最大值是 .

【答案】5![]() cm
cm
【解析】
试题分析:只有BF大于等于AB时,B′才会落在AD上,判断出点F与点C重合时,折痕EF最大,根据翻折的性质可得BC=B′C,然后利用勾股定理列式求出B′D,从而求出AB′,设BE=x,根据翻折的性质可得B′E=BE,表示出AE,在Rt△AB′E中,利用勾股定理列方程求出x,再利用勾股定理列式计算即可求出EF.
解:如图,点F与点C重合时,折痕EF最大,
由翻折的性质得,BC=B′C=10cm,
在Rt△B′DC中,B′D=![]() =
=![]() =6cm,
=6cm,
∴AB′=AD﹣B′D=10﹣6=4cm,
设BE=x,则B′E=BE=x,
AE=AB﹣BE=8﹣x,
在Rt△AB′E中,AE2+AB′2=B′E2,
即(8﹣x)2+42=x2,
解得x=5,
在Rt△BEF中,EF=![]() =
=![]() =5
=5![]() cm.
cm.
故答案为:5![]() cm.
cm.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目