题目内容
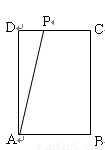
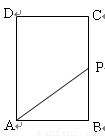
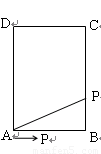
如图,长方形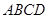 中,
中,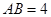 cm,
cm,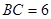 cm,现有一动点
cm,现有一动点 从
从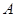 出发以2cm/秒的速度,沿矩形的边
出发以2cm/秒的速度,沿矩形的边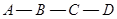 回到点
回到点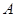 ,设点
,设点 运动的时间为
运动的时间为 秒.
秒.

(1)当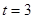 秒时,求
秒时,求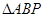 的面积;
的面积;
(2)当 为何值时,点
为何值时,点 与点
与点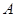 的距离为5cm?
的距离为5cm?
(3)当 为何值时
为何值时 ,以线段
,以线段 、
、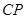 、
、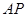 的长度为三边长的三角形是直角三角形,且
的长度为三边长的三角形是直角三角形,且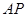 是斜边.
是斜边.
【答案】
(1)当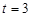 时,点
时,点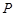 的路程为
的路程为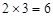 cm …………………(1分)
cm …………………(1分)
∵ 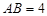 cm,
cm,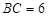 cm
cm
∴ 点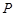 在
在 上
上
∴ 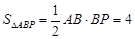 ………………………………(3分)
………………………………(3分)
(2)
(Ⅰ)若点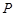 在
在 上
上
∵ 在Rt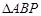 中,
中,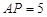 ,
,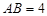
∴ 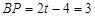
∴ 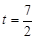 …………………………………………………(5分)
…………………………………………………(5分)
(Ⅱ)若点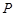 在
在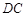 上,则在Rt
上,则在Rt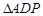 中,
中,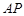 是斜边
是斜边
∵ 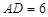 ∴
∴ 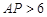 ∴
∴ 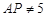 ……………(6分)
……………(6分)
(Ⅲ)若点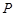 在
在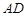 上,
上,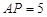
则点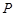 的路程为
的路程为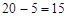
∴ 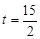 ………………………………………………(8分)
………………………………………………(8分)
综上,当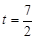 秒或
秒或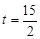 时,
时,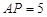 cm. ……………(9分)
cm. ……………(9分)
(3)当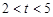 时,点
时,点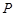 在
在 边上
边上
∵ 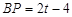 ,
, …………………………(10分)
…………………………(10分)
∴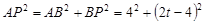
由题意,有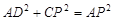
∴ 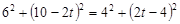
∴ 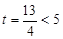 ……………………………………………(12分)
……………………………………………(12分)
【解析】
试题分析:(1)首先算出P点经过的路程,然后P点在BC上,然后利用直角三角形的面积公式求出结果;
(2)分点P在AB、DC、AD边三种情况进行讨论;
(3)首先确定P 点在BC边上,然后利用勾股定理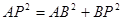 列出方程,然后根据二次函数的性质求出t的值.
列出方程,然后根据二次函数的性质求出t的值.
考点:勾股定理;二次函数性质.
点评:此题要求对P点所经过的位置进行分析讨论,然后运用勾股定理计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

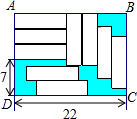 如图,长方形ABCD中放置9个形状大小都相同的小长方形,尺寸如图,单位:cm求图中阴影部分面积.
如图,长方形ABCD中放置9个形状大小都相同的小长方形,尺寸如图,单位:cm求图中阴影部分面积. 中,
中, cm,
cm,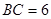 cm,现有一动点
cm,现有一动点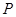 从
从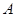 出发以2cm/秒的速度,沿矩形的边
出发以2cm/秒的速度,沿矩形的边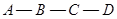 回到点
回到点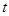 秒.
秒.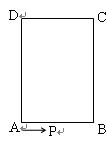
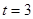 秒时,求
秒时,求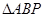 的面积;
的面积; ,以线段
,以线段 、
、 、
、 的长度为三边长的三角形是直角三角形,且
的长度为三边长的三角形是直角三角形,且