题目内容
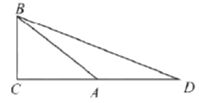
【题目】(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
【答案】(1)![]() 或
或![]() (2)
(2)![]() ;
;![]() (3)
(3)![]() 或
或![]()
【解析】
(1)过点P作PE⊥BC于E,得到AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,利用勾股定理得到方程,故可求解;
(2)根据运动时间求出EQ、PE,利用勾股定理即可求解;
(3) 分当点P在AO上时,当点P在OC上时和当点P在CB上时,根据三角形的面积公式列出方程即可求解.
解:(1)设运动时间为t秒时,如图,过点P作PE⊥BC于E,
由运动知,AP=3t,CQ=2t,PE=6,EQ=16﹣3t﹣2t=16﹣5t,
∵点P和点Q之间的距离是10 cm,
∴62+(16﹣5t)2=100,
解得t1=![]() ,t2=
,t2=![]() ,
,
∴t=![]() 或
或![]() .
.
故答案为![]() 或
或![]()
(2)t=2时,由运动知AP=3×2=6 cm,CQ=2×2=4 cm,
∴四边形APEB是矩形,
∴PE=AB=6,BE=6,
∴EQ=BC﹣BE﹣CQ=16﹣6﹣4=6,
根据勾股定理得PQ=![]() ,
,
∴当t=2 s时,P,Q两点的距离为6![]() cm;
cm;
当t=4 s时,由运动知AP=3×4=12 cm,CQ=2×4=8cm,
∴四边形APEB是矩形,
∴PE=AB=6,BQ=8,CE=OP=4
∴EQ
根据勾股定理得PQ=![]() ,
,
P,Q两点的距离为2![]() cm.
cm.
(3)点Q从C点移动到B点所花的时间为16÷2=8s,
当点P在AO上时,S△POQ=![]() =
=![]() =12,
=12,
解得t=4.
当点P在OC上时,S△POQ=![]() =
=![]() =12,
=12,
解得t=6或﹣![]() (舍弃).
(舍弃).
当点P在CB上时,S△POQ=![]() =
=![]() =12,
=12,
解得t=18>8(不符合题意舍弃),
综上所述,经过4 s或6 s时,△POQ的面积为12 cm2.