题目内容
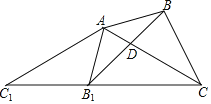
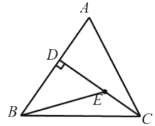
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 的一个动点,则
的一个动点,则![]() 的最小值是________.
的最小值是________.
【答案】![]()
【解析】
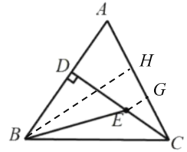
作EG⊥AC于G,BH⊥AC于H,由tanA=![]() =3,设AD=a,CD=3a,利用勾股定理构建方程求出a,再证明EG=
=3,设AD=a,CD=3a,利用勾股定理构建方程求出a,再证明EG=![]() EC,推出BE+
EC,推出BE+![]() EC=BE+EG,由垂线段最短即可解决问题.
EC=BE+EG,由垂线段最短即可解决问题.
解:如图,作EG⊥AC于G,BH⊥AC于H,
∵CD⊥AB,
∴∠ADC=90°,
∵tanA=![]() =3,设AD=a,CD=3a,
=3,设AD=a,CD=3a,
∵AB=AC=10,
则有:102=a2+9a2,
∴a2=10,
∴a=![]() 或
或![]() (舍),
(舍),
∴CD=3a=![]() ,
,
∵AB=AC,CD⊥AB,BH⊥AC,
∴BH=CD=![]() ,
,
∵∠ECG=∠ACD,∠CGE=∠CDA,
∴sin∠ECG=![]() =
=![]() =
=![]() ,
,
∴EG=![]() EC,
EC,
∴BE+![]() EC=BE+EG,
EC=BE+EG,
∴BE+EG≥BH,
∴BE+![]() EC≥
EC≥![]() ,
,
∴BE+![]() EC的最小值为
EC的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目