题目内容
方程
+
=12的实数解个数为（ ）
| x+19 |
| 3 | x+95 |
| A、0 | B、1 | C、2 | D、3 |
分析：首先由题意可知，x+19是完全平方数，x+95是立方数，然后利用分类讨论思想求解即可．
解答：解：由题意得：x+19≥0，
∴x≥-19，
∴x+95≥76，
∵
+
=12，
∴x+19是完全平方数，且x+19＜144，
∴当x+19=0时，
不是有理数，舍去，
当x+19=1时，
不是有理数，舍去，
当x+19=4时，
不是有理数，舍去，
当x+19=9时，
不是有理数，舍去，
当x+19=16时，
不是有理数，舍去，
当x+19=25时，
不是有理数，舍去，
当x+19=36时，
不是有理数，舍去，
当x+19=49时，
=5，符合题意，此时x=30；
当x+19=64时，
=8，
＞5，此时8+5＞12，
∴当x+19＞64时，不符合题意．
故方程
+
=12的实数解个数为1个．
故选B．
∴x≥-19，
∴x+95≥76，
∵
| x+19 |
| 3 | x+95 |
∴x+19是完全平方数，且x+19＜144，
∴当x+19=0时，
| 3 | 76 |
当x+19=1时，
| 3 | 77 |
当x+19=4时，
| 3 | 80 |
当x+19=9时，
| 3 | 85 |
当x+19=16时，
| 3 | 92 |
当x+19=25时，
| 3 | 101 |
当x+19=36时，
| 3 | 112 |
当x+19=49时，
| 3 | 125 |
当x+19=64时，
| x+19 |
| 3 | 140 |
∴当x+19＞64时，不符合题意．
故方程
| x+19 |
| 3 | x+95 |
故选B．
点评：此题考查了无理方程的实数根问题．注意抓住完全平方数是解此题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
．
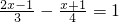