题目内容
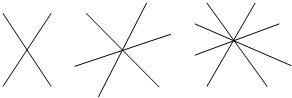 如图:
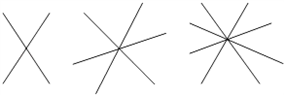
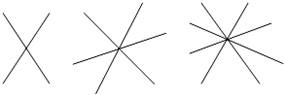
如图:两条直线相交于一点形成
三条直线相交于一点形成
四条直线相交于一点形成
请你写出n条直线相交于一点可形成
分析:两条直线相交于一点形成2对对顶角,很明显,三、四、n条直线相交于一点可看成是3、6、
种两条直线相交于一点的情况,再乘以2,即可得对顶角的对数.
| n(n-1) |
| 2 |
解答:解:两条直线相交于一点形成2对对顶角;
三条直线相交于一点可看成是三种两条直线相交于一点的情况,所以形成6对对顶角;
四条直线相交于一点可看成是六种两条直线相交于一点的情况,所以形成12对对顶角;
n条直线相交于一点可看成是
种两条直线相交于一点的情况,所以形成n(n-1)对对顶角.
三条直线相交于一点可看成是三种两条直线相交于一点的情况,所以形成6对对顶角;
四条直线相交于一点可看成是六种两条直线相交于一点的情况,所以形成12对对顶角;
n条直线相交于一点可看成是
| n(n-1) |
| 2 |
点评:本题是一个探索规律型的题目,解决时注意观察每对数之间的关系.这是中考中经常出现的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
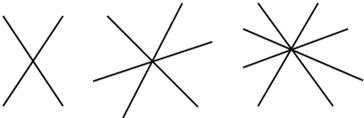
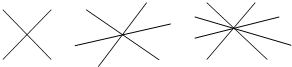 如图:两条直线相交于一点形成2对对顶角,三条直线相交于一点形成6对对顶角,四条直线相交于一点形成12对对顶角,请你写出n条直线相交于一点可形成
如图:两条直线相交于一点形成2对对顶角,三条直线相交于一点形成6对对顶角,四条直线相交于一点形成12对对顶角,请你写出n条直线相交于一点可形成