题目内容
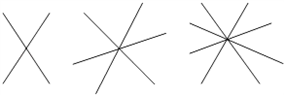
19、如图:
两条直线相交于一点形成2对对顶角,
三条直线相交于一点形成6对对顶角,
四条直线相交于一点形成12对对顶角,
请你写出n条直线相交于一点可形成
两条直线相交于一点形成2对对顶角,
三条直线相交于一点形成6对对顶角,
四条直线相交于一点形成12对对顶角,
请你写出n条直线相交于一点可形成
n(n-1)
对对顶角.
分析:结合图形,可以从特殊推广到一般,即两条直线相交于一点形成2对对顶角,即2=2×1;三条直线相交于一点形成6对对顶角,即6=3×2;四条直线相交于一点形成12对对顶角,即12=4×3,推而广之即可.
解答:解:根据2=2×1,6=3×2,12=4×3,则n条直线相交于一点可形成n(n-1)对对顶角.
故答案为n(n-1).
故答案为n(n-1).
点评:此题是一道规律题,能够从特殊推广到一般.

练习册系列答案
相关题目
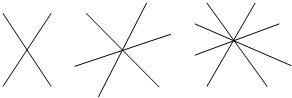 如图:
如图: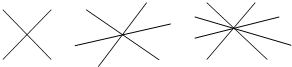 如图:两条直线相交于一点形成2对对顶角,三条直线相交于一点形成6对对顶角,四条直线相交于一点形成12对对顶角,请你写出n条直线相交于一点可形成
如图:两条直线相交于一点形成2对对顶角,三条直线相交于一点形成6对对顶角,四条直线相交于一点形成12对对顶角,请你写出n条直线相交于一点可形成