题目内容
如图，矩形ABCD的边AB在y轴上，点O为AB的中点．已知AB=4，边CD交x轴于点E．则点C的坐标为
- A.（3，2）
- B.（2，3）
- C.（3，-2）
- D.（-3，-2）
C
分析：根据坐标与正方形四边相等的性质可知道可知BC=3，CE=2，又C在第四象限所以可求得C点坐标．
解答：∵四边形ABCD为矩形，AB=4，点O为AB的中点，
∴BC=3，CE=2，
又C点在第三象限，
∴C点坐标为（3，-2）．
故选C．
点评：本题考查坐标与图形性质的知识，要熟悉正方形四边相等且每个角都是90°的性质和象限的知识．
分析：根据坐标与正方形四边相等的性质可知道可知BC=3，CE=2，又C在第四象限所以可求得C点坐标．
解答：∵四边形ABCD为矩形，AB=4，点O为AB的中点，
∴BC=3，CE=2，
又C点在第三象限，
∴C点坐标为（3，-2）．
故选C．
点评：本题考查坐标与图形性质的知识，要熟悉正方形四边相等且每个角都是90°的性质和象限的知识．
练习册系列答案
相关题目
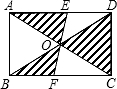如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=2，BC=3，则图中阴影部分的面积为
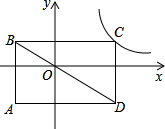如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=
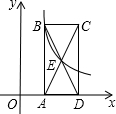如图，矩形ABCD的一边AD在x轴上，对角线AC、BD交于点E，过B点的双曲线
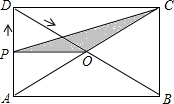（2013•葫芦岛）如图，矩形ABCD的对角线交于点O，∠BOC=60°，AD=3，动点P从点A出发，沿折线AD-DO以每秒1个单位长的速度运动到点O停止．设运动时间为x秒，y=S△POC，则y与x的函数关系大致为（ ）
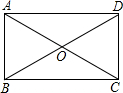如图，矩形ABCD的对角线交于O点，∠AOB=120°，AD=5cm，则AC=