题目内容
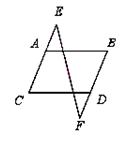
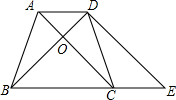
如图,在等腰梯形ABCD中,已知AD//BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE。
(1)求证:BD=DE。
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长。
(1)求证:BD=DE。
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长。

(1)见解析(2)

解:(1)证明:∵AD∥BC,CE=AD,∴四边形ACED是平行四边形。
∴AC=DE。
∵四边形ABCD是等腰梯形,AD∥BC,AB=DC,∴AC=BD。
∴BD=DE。
(2)过点D作DF⊥BC于点F,
∵四边形ACED是平行四边形,∴CE=AD=3,AC∥DE。
∵AC⊥BD,∴BD⊥DE。
∵BD=DE,
∴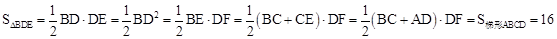 。
。
∴BD=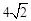 。∴BE=
。∴BE=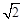 BD=8。∴DF=BF=EF=
BD=8。∴DF=BF=EF=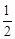 BE=4。∴CF=EF-CE=1。
BE=4。∴CF=EF-CE=1。
∴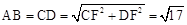 。
。
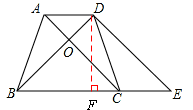
(1)由AD∥BC,CE=AD,可得四边形ACED是平行四边形,即可证得AC=DE,又由等腰三角形的性质,可得AC=BD,即可证得结论。
(2)过点D作DF⊥BC于点F,可证得△BDE是等腰直角三角形,由SABCD=16,可求得BD的长,从而求得答案。
∴AC=DE。
∵四边形ABCD是等腰梯形,AD∥BC,AB=DC,∴AC=BD。
∴BD=DE。
(2)过点D作DF⊥BC于点F,
∵四边形ACED是平行四边形,∴CE=AD=3,AC∥DE。
∵AC⊥BD,∴BD⊥DE。
∵BD=DE,
∴
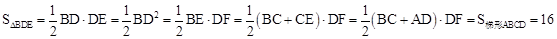 。
。∴BD=
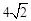 。∴BE=
。∴BE=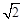 BD=8。∴DF=BF=EF=
BD=8。∴DF=BF=EF=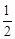 BE=4。∴CF=EF-CE=1。
BE=4。∴CF=EF-CE=1。∴
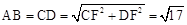 。
。
(1)由AD∥BC,CE=AD,可得四边形ACED是平行四边形,即可证得AC=DE,又由等腰三角形的性质,可得AC=BD,即可证得结论。
(2)过点D作DF⊥BC于点F,可证得△BDE是等腰直角三角形,由SABCD=16,可求得BD的长,从而求得答案。

练习册系列答案
相关题目

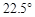 角
角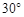 角
角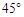 角
角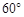 角
角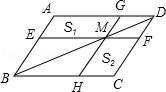
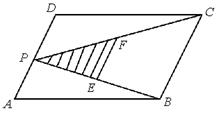
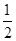 FD,EF交AC于G,则AG︰AC=______.
FD,EF交AC于G,则AG︰AC=______.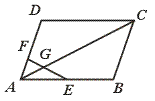
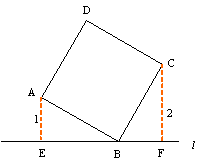
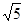 C.
C.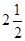 D.以上都不对
D.以上都不对 ABCD的两条对角线AC、BD相交于点
ABCD的两条对角线AC、BD相交于点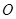 ,
,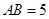 ,
,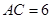 ,
,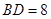 ,则
,则
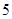 B.
B.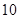 C.
C.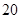 D.
D.