题目内容
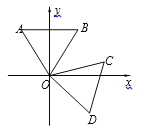
【题目】如图,等边△OAB的顶点O为坐标原点,AB∥x轴,OA=2,将等边△OAB绕原点O顺时针旋转105至△OCD的位置,则点D的坐标为( )
A.(2,-2)B.(![]() ,
,![]() )C.(
)C.(![]() ,
,![]() )D.(
)D.(![]() ,
,![]() )
)
【答案】D
【解析】
过点D向x轴作垂线,垂足为E,根据等边三角形的性质以及直线平行的性质证明△EOD是等腰直角三角形,再根据等边三角形的边长以及D点在第四象限即可得到答案.
解:如图,过点D向x轴作垂线,垂足为E,

∵△OAB是等边三角形,旋转角是105°,
∴∠AOB=∠B=∠COD =60°,∠AOC=105°,
∴∠BOC=∠AOC-∠AOB=105°-60°=45°,
又∵AB∥x轴,
∴∠BOE=∠B=60°(两直线平行,内错角相等),
∴∠COE=∠BOE-∠BOC=60°-45°=15°,
∴∠EOD=∠DOC-∠COE=60°-15°=45°,
∴△EOD是等腰直角三角形,
∴![]()
∵OD=OA=2,
∴![]() (勾股定理),
(勾股定理),
∴![]()
∵D点在第四象限,
∴D点的坐标为:(![]() ,
,![]() )
)
故选D;

 阅读快车系列答案
阅读快车系列答案【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对本校甲、乙两班各60名学生进行了垃极分类相关知识的测试,并分别随机抽取了15份成绩,整理分析过程如下,请补充完整
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
按如下分数段整理、描述这两组样本数据
组别 班级 | 65.6~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲班 | 2 | 2 | 4 | 5 | 1 | 1 |
乙班 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲班 | 80 | x | 80 | 47.6 |
乙班 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(2)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类相关知识合格的学生有 人
(3)你认为哪个班的学生掌握垃圾分类相关知识的情况较好,说明理由.