题目内容
平行四边形的两条对角线长分别是x,y,一边长为12,则x,y可能是下列各组中的( )
| A、8与14 | B、10与14 | C、18与20 | D、10与38 |
分析:由平行四边形的两条对角线长分别是x,y,一边长为12,根据平行线的性质与三角形三边关系,即可得
x+
y>12,|
y-
x|<12,然后验证即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: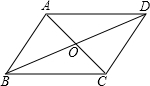 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OA=OC=
AC=
x,OB=OD=
BD=
y,BC=12,
根据三角形三边关系可得:
x+
y>12,|
y-
x|<12,
即:x+y>24,|x-y|<24,
然后代入数值检验.即可得C符合要求.
故选C.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
根据三角形三边关系可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即:x+y>24,|x-y|<24,
然后代入数值检验.即可得C符合要求.
故选C.
点评:此题考查了平行四边形的性质与三角形的三边关系.解题的关键是注意数形结合思想与方程思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目