题目内容
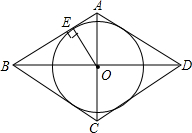 如图,菱形ABCD中,对角线AC,BD相交于O点,OE⊥AB,垂足为E,以O为圆心,OE为半径作⊙O.试说明⊙O与CD相切.
如图,菱形ABCD中,对角线AC,BD相交于O点,OE⊥AB,垂足为E,以O为圆心,OE为半径作⊙O.试说明⊙O与CD相切.分析:AB∥CD OE⊥AB 延长EO交CD于点F.因为菱形ABCD的对边AB∥CD,且OF⊥CD.所以,只需通过面积法求得OE=OF即可.
解答: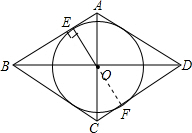 证明:如图,延长EO交CD于点F.
证明:如图,延长EO交CD于点F.
∵在菱形ABCD中,AB∥CD,OE⊥AB,
∴OF⊥CD.
∵在菱形ABCD中,OA=OC,OB=OD,AC⊥BD,AB=CD,
∴S△AOB=
OA•OB=
OC•OD=S△COD,即
AB•OE=
CD•OF,
∴OE=OF.
∵OE为⊙O的半径,
∴OF是⊙O的半径,
∴⊙O与CD相切.
 证明:如图,延长EO交CD于点F.
证明:如图,延长EO交CD于点F.∵在菱形ABCD中,AB∥CD,OE⊥AB,
∴OF⊥CD.
∵在菱形ABCD中,OA=OC,OB=OD,AC⊥BD,AB=CD,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=OF.
∵OE为⊙O的半径,
∴OF是⊙O的半径,
∴⊙O与CD相切.
点评:本题考查了切线的判定.切线的判定定理实际上是从”圆心到直线的距离等于半径时,直线和圆相切“这个结论直接得出来的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
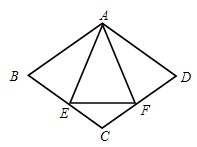 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
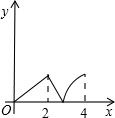
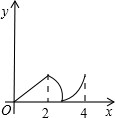
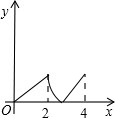
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.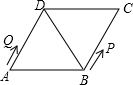 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )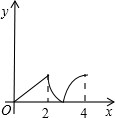
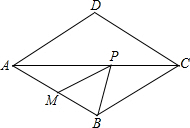 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2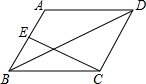 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.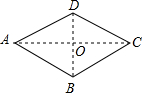 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,