题目内容
直线y="k" x+b经过一、二、四象限,则k、b应满足 ( )
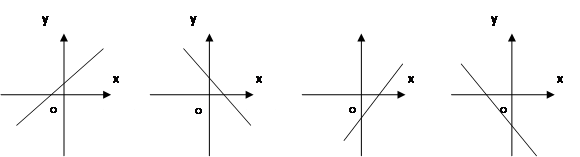

| A. k>0, b<0 | B. k>0,b>0 | C. k<0, b<0 | D.k<0, b>0 |
D
分析:根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k,b的取值范围,从而求解.
解答:解:由一次函数y=kx+b的图象经过第一、二、四象限,
又由k<0时,直线必经过二、四象限,故知k<0.
再由图象过一、二象限,即直线与y轴正半轴相交,所以b>0.
故选D.
解答:解:由一次函数y=kx+b的图象经过第一、二、四象限,
又由k<0时,直线必经过二、四象限,故知k<0.
再由图象过一、二象限,即直线与y轴正半轴相交,所以b>0.
故选D.

练习册系列答案
相关题目
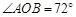 ,则
,则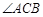 的度数是
的度数是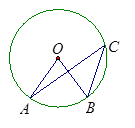
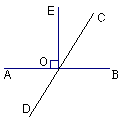

 的补角是
的补角是 ,则
,则 度
度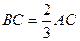 ,D为BC的中点,求BC、AD的长
,D为BC的中点,求BC、AD的长