题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)若![]() 两点中只有一个点在线段
两点中只有一个点在线段![]() 上,直接写出
上,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据对称的性质直接得出点B的坐标即可;
(2)分别联立直线![]() 与一次函数
与一次函数![]() 的解析式,直线
的解析式,直线![]() 与与反比例函数
与与反比例函数![]() 的解析式,求解即可;
的解析式,求解即可;
(3)先求出直线AB的解析式为y=1,再根据若P(m-1,1),Q(m,1)其中只有一个点在线段AB上可得①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,求解即可.
,求解即可.
解:(1)∵A(1,1)与点B关于y轴对称,
∴B的坐标为:(-1,1);
(2)联立直线![]() 与一次函数
与一次函数![]() 的解析式,
的解析式,
得![]() ,
,
解得![]() ,
,
∴P的坐标为(m-1,1),
联立直线![]() 与与反比例函数
与与反比例函数![]() 的解析式,
的解析式,
得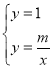 ,
,
解得![]() ,
,
∴Q的坐标为(m,1);
(3)∵A(1,1),B(-1,1),
∴直线AB的解析式为y=1,
若P(m-1,1),Q(m,1)其中只有一个点在线段AB上,则有:
①![]() ,
,
此时不等式组无解;
②![]() ,
,
解得1<m≤2;
③![]() ,
,
解得-1≤m<0;
④![]() ,
,
此时不等式组无解;
综上所述,m的取值范围是![]() 或
或![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目