题目内容
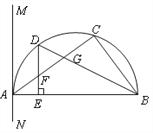
【题目】如图,⊙O的直径AB=2,AM、BN是它的两条切线,CD与⊙O相切于点E,与BN、AM交于点C、D,设AD=x,BC=y。
(1)求证:AM∥BN。
(2)求y关于x的函数关系式。
(3)若x、y是关于t的方程2t![]() -5t+m=0的两根,且xy=
-5t+m=0的两根,且xy=![]() ,求x、y的值。
,求x、y的值。

【答案】(1)详见解析;(2)y=![]() (x>0);(3)x=
(x>0);(3)x=![]() ,y=2.
,y=2.
【解析】试题分析:(1)由AM和BN是⊙O的两条切线,可得AB⊥AD,AB⊥BC,则可证得AM∥BN.
(2)首先作DF⊥BN交BC于F,可得四边形ABFD是矩形,然后根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
(3)解一元二次方程即可求得结果.
试题解析:(1)证明:∵AM和BN是⊙O的两条切线,
∴AB⊥AD,AB⊥BC,
∴AM∥BN.
(2)解:作DF⊥BN交BC于F,

∵AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=2,
∵BC=y,
∴FC=BC-BF=y-x;
∵AM和BN是⊙O的两条切线,DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(x-y)2+22,
整理为:y=![]() ,
,
∴y与x的函数关系为:y=![]() .
.
(3)由xy=![]() 及(2)问的结论,
及(2)问的结论,
得xy=![]() =1,m=2
=1,m=2
所以原方程可以转化为2t![]() -5t+2=0,
-5t+2=0,
即(t-2)(2t-1)=0,解得t=2或t=![]() .
.
因为x<y,所以x=![]() ,y=2.
,y=2.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目