题目内容
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 于
于![]() ,
,![]() 于
于![]() ,并且
,并且![]() ,动点
,动点![]() 以
以![]() 的速度从
的速度从![]() 点向
点向![]() 点运动,动点
点运动,动点![]() 以
以![]() 的速度从点
的速度从点![]() 向点
向点![]() 运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为
运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为![]() .
.
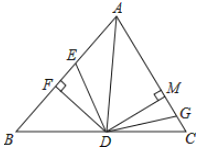
(1)求证:在运动过程中,不管![]() 取何值,都有
取何值,都有![]() ;
;
(2)当![]() 取何值时,
取何值时,![]() 与
与![]() 全等;
全等;
(3)若![]() ,当
,当![]() 时
时![]() ,求此时
,求此时![]() 的面积
的面积![]() .
.
【答案】(1)证明见解析;(2)当![]() 时,△DFE与△DMG全等;(3)
时,△DFE与△DMG全等;(3)![]()
【解析】
(1)由角平分线的性质可知DF=DM,所以△AED和△DGC的面积转化为底AE和CG的比值,根据路程=速度×时间求出AE和CG的长度即可证明在运动过程中,不管取何值,都有![]() ;
;
(2)分两种情况进行讨论:①当0<t<3时,②当3<t<5时,分别根据△DFE≌△DMG,得出EF=GM,据此列出关于t的方程,进行求解即可;
(3)利用等高三角形的面积比等于对应底的比,即可求得答案.
(1)∵![]() 是
是![]() 的平分线, DF⊥AB,DM⊥AC,
的平分线, DF⊥AB,DM⊥AC,
∴DF=DM,
∵![]()
∴![]() ,
,
∵点E以3cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴在运动过程中,不管取何值,都有![]() .
.
(2)∵![]() 是
是![]() 的平分线, DF⊥AB,DM⊥AC,
的平分线, DF⊥AB,DM⊥AC,
∴![]() ,
,
∴![]() ,
,
①当0<t<3时,点G在线段CM上,点E在线段AF上. ![]() ,
,
∴![]() ,
,
∴![]() (不合题意,舍去);
(不合题意,舍去);
②当3<t<5时,点G在线段AM上,点E在线段AF上.![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述当![]() 时,△DFE与△DMG全等;
时,△DFE与△DMG全等;
(3)∵![]() ,
,
∴![]() (
(![]() ),
),
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() (
(![]() ),
),
∴![]() (
(![]() ),
),
∵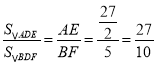 ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目