题目内容
【题目】如图,AB是⊙O的直径,D为圆周上任一点,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
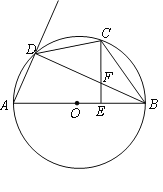
(1)求证:![]() ;
;
(2)若![]() ,⊙O的半径为3,求BC的长.
,⊙O的半径为3,求BC的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
试题分析:连接AC,根据已知条件利用等角对等边可以得到CF=BF;作CG⊥AD于点G,先利用HL判定Rt△BCE≌Rt△DCG,推出BE=DG,根据边之间的关系可求得BE的值,再根据相似三角形的判定得到△BCE∽△BAC,根据相似三角形的对应边成比例,可得到BC2=BEAB,这样便求得BC的值,注意负值要舍去.
试题解析:(1)连接AC,如图
∵C是弧BD的中点
∴∠BDC=∠DBC
又∵∠BDC=∠BAC
在△ABC中,∠ACB=90°,CE⊥AB
∴∠BCE=∠BAC
∠BCE=∠DBC
∴CF=BF;
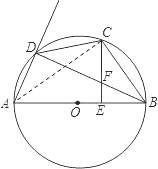
(2)作CG⊥AD于点G,

∵C是弧BD的中点
∴∠CAG=∠BAC,
即AC是∠BAD的角平分线.
∴CE=CG,AE=AG
在Rt△BCE与Rt△DCG中,
CE=CG,CB=CD
∴Rt△BCE≌Rt△DCG(HL)
∴BE=DG
∴AE=AB-BE=AG=AD+DG
即6-BE=2+DG
∴2BE=4,即BE=2
又∵△BCE∽△BAC
∴BC2=BEAB=12
BC=±2![]() (舍去负值)
(舍去负值)
∴BC=2![]() .
.

练习册系列答案
相关题目