��Ŀ����
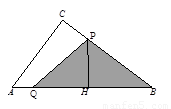
��֪����ͼ����ABC�У���C��90�㣬AC��3���ף�CB��4���ף���������P��Q�ֱ��A��C����ͬʱ��˳ʱ�뷽���ء�ABC�ı��˶�������Q�˶�����Aʱ��P��Q�����˶���ֹͣ����P��Q���˶��ٶȷֱ�Ϊ1����/�롢2����/�룬���P�˶�ʱ��Ϊ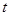 ���룩��
���룩��
��1����ʱ��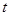 Ϊ��ֵʱ����P��C��Q����Ϊ����������ε������ͼ�е���Ӱ���֣�����2����2��
Ϊ��ֵʱ����P��C��Q����Ϊ����������ε������ͼ�е���Ӱ���֣�����2����2��
��2������P��Q�˶�ʱ����Ӱ���ֵ���״��֮�仯����PQ���ABCΧ����Ӱ�������ΪS������2�������S��ʱ��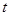 �ĺ�����ϵʽ����ָ���Ա���
�ĺ�����ϵʽ����ָ���Ա���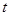 ��ȡֵ��Χ��
��ȡֵ��Χ��
 ��3����P��Q���˶��Ĺ����У���Ӱ�������S�����ֵ�����У���������ֵ����û�У���˵�����ɣ�
��3����P��Q���˶��Ĺ����У���Ӱ�������S�����ֵ�����У���������ֵ����û�У���˵�����ɣ�

��1��S��PCQ�� PC��CQ��
PC��CQ��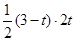 ��
��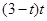 ��2��
��2��
��������á� ��1��
��1�� ��2
��2
�൱ʱ��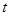 Ϊ1���2��ʱ��S��PCQ��2����2��
Ϊ1���2��ʱ��S��PCQ��2����2��
��2���ٵ�0��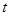 ��2ʱ��S��
��2ʱ��S�� ��
��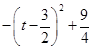 ��
��
�� �ڵ�2��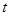 ��3ʱ�� S��
��3ʱ�� S�� ��
��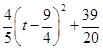 ��
��
�� �۵�3��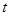 ��4.5ʱ��S��
��4.5ʱ��S��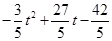 ��
��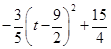 ��
��
��3����
����0��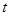 ��2ʱ����
��2ʱ����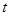 ��
��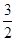 ��S�����ֵ��S1��
��S�����ֵ��S1��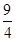 ��
��
����
����2��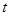 ��3ʱ����
��3ʱ����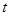 ��3��S�����ֵ��S2��
��3��S�����ֵ��S2��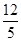 ��
��

����3��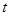 ��4.5ʱ����
��4.5ʱ����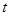 ��
��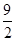 ��S�����ֵ��S3��
��S�����ֵ��S3��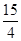 ��
��
��S1��S2��S3����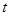 ��
��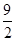 ʱ��S�����ֵ��S���ֵ��
ʱ��S�����ֵ��S���ֵ��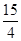 ��
��
����������1������PC=3��t��CQ=2t����C=90�㣬�ɱ�ʾS��PCQ���Ӷ����t��ֵ��
��2�������˶�״̬�������ֿ���������ٵ�0��t��2ʱ���ڵ�2��t��3ʱ���۵�3��t��4.5ʱ���ֱ��ʾ��Ӱ����������ڢ��У�S=S��ABC��S��APQ���ɣ���C=90�㣬AC=3���ף�CB=4���ף��ù��ɶ�������AB=5���ף���AB���ϵĸ�PH���������Ʊȱ�ʾPH���ٱ�ʾ�����
��3���ã�2���Ľ��ۣ��ֱ����ÿһ������µ����ֵ��ע���Ա���ȡֵ��Χ�����ٱȽϣ�������������е����ֵ��

 ��У����ϵ�д�
��У����ϵ�д� 17����֪����ͼ����ABC�У���BAC=90�㣬AD��BC�ڵ�D��BEƽ�֡�ABC����AD�ڵ�M��ANƽ�֡�DAC����BC�ڵ�N��
17����֪����ͼ����ABC�У���BAC=90�㣬AD��BC�ڵ�D��BEƽ�֡�ABC����AD�ڵ�M��ANƽ�֡�DAC����BC�ڵ�N�� ��֪����ͼ����ABC����ACB ��ƽ�����ཻ�ڵ�F����F��DE��BC��D����AC ��E����AB=6��AC=5����������ADE���ܳ���
��֪����ͼ����ABC����ACB ��ƽ�����ཻ�ڵ�F����F��DE��BC��D����AC ��E����AB=6��AC=5����������ADE���ܳ��� ��֪����ͼ����ABC�ǵȱ������Σ���D��AB�ϣ���E��AC���ӳ����ϣ���BD=CE��DE��BC��F����֤��BF=CF+CE��
��֪����ͼ����ABC�ǵȱ������Σ���D��AB�ϣ���E��AC���ӳ����ϣ���BD=CE��DE��BC��F����֤��BF=CF+CE�� ��֪����ͼ����ABC�У�AB=AC=10��BC=16����D��BC�ϣ�DA��CA��A��
��֪����ͼ����ABC�У�AB=AC=10��BC=16����D��BC�ϣ�DA��CA��A�� ��֪����ͼ����ABC�У�AD��BC��BD=DE����E��AC�Ĵ�ֱƽ�����ϣ�
��֪����ͼ����ABC�У�AD��BC��BD=DE����E��AC�Ĵ�ֱƽ�����ϣ�