题目内容
(2009•乐山)如图,∠AOB=30°,过OA上到点O的距离为1,3,5,7,…的点作OA的垂线,分别与OB相交,得到如图所示的阴影梯形,它们的面积依次记为S1,S2,S3,….则:(1)S1= ;
(2)通过计算可得S2009= .

【答案】分析:(1)分析知奇数的通式为:2n-1(n为正整数),设阴影梯形的上底和下底距点O的长分别为a和b,则可以表达出Sn的表达式,将每个梯形的上底和下底距点O的长代入,求解即可;
(2)第2009个梯形前面已有2008×2个奇数,2009个梯形上底距点O的距离为第2008×2+1个奇数,下底为第2008×2+2个奇数.
解答:解:(1)设阴影梯形的上底和下底距点O的长分别为a和b,
则Sn= b×btan∠AOB-
b×btan∠AOB- a×atan∠AOB=
a×atan∠AOB= (b2-a2),
(b2-a2),
又∵梯形1距离点O的距离a=1,b=3,
∴S1= (32-12)=
(32-12)=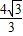 ;
;
(2)第2009个梯形前面已有2008×2个奇数,
2009个梯形上底距点O的距离为第2008×2+1个奇数,
下底为第2008×2+2个奇数,
∴第2009个梯形的两边长分别为:
a=2×(2008×2+1)-1=8033,
b=2×(2008×2+1)+1=8035,
故S2009= (80352-80332)=5356
(80352-80332)=5356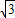 .
.
点评:本题考查学生分析、探究问题及运用规律解决问题的能力.有一定难度.
(2)第2009个梯形前面已有2008×2个奇数,2009个梯形上底距点O的距离为第2008×2+1个奇数,下底为第2008×2+2个奇数.
解答:解:(1)设阴影梯形的上底和下底距点O的长分别为a和b,
则Sn=
 b×btan∠AOB-
b×btan∠AOB- a×atan∠AOB=
a×atan∠AOB= (b2-a2),
(b2-a2),又∵梯形1距离点O的距离a=1,b=3,
∴S1=
 (32-12)=
(32-12)=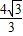 ;
;(2)第2009个梯形前面已有2008×2个奇数,
2009个梯形上底距点O的距离为第2008×2+1个奇数,
下底为第2008×2+2个奇数,
∴第2009个梯形的两边长分别为:
a=2×(2008×2+1)-1=8033,
b=2×(2008×2+1)+1=8035,
故S2009=
 (80352-80332)=5356
(80352-80332)=5356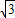 .
.点评:本题考查学生分析、探究问题及运用规律解决问题的能力.有一定难度.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
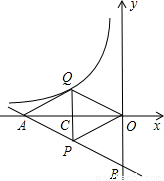
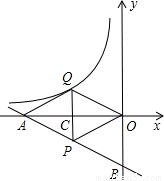
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
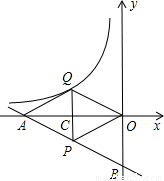
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=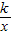 (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
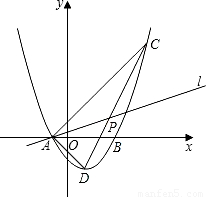
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=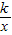 (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
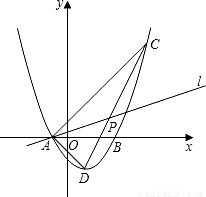
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=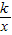 (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.