题目内容
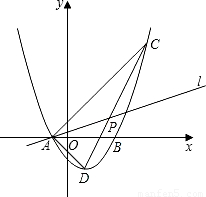
(2009•乐山)如图,在平面直角坐标系中,开口向上的抛物线与x轴交于A、B两点,D为抛物线的顶点,O为坐标原点.若OA、OB(OA<OB)的长分别是方程x2-4x+3=0的两根,且∠DAB=45°.(1)求抛物线对应的二次函数解析式;
(2)过点A作AC⊥AD交抛物线于点C,求点C的坐标;
(3)在(2)的条件下,过点A任作直线l交线段CD于点P,若点C、D到直线l的距离分别记为d1、d2,试求的d1+d2的最大值.
【答案】分析:(1)通过解方程即可求得OA、OB的长,从而得到点A、B的坐标,由于A、B关于抛物线的对称轴对称,且∠DAB=45°,那么△DAB是等腰直角三角形,即可利用点A、B的坐标求得点D的坐标,然后根据待定系数法求得抛物线的解析式;
(2)由于AC⊥AD,且∠DAB=45°,则∠CAB=45°,设出点C的横坐标,那么其纵坐标应为m+1,然后将C点坐标代入抛物线的解析式中,即可求得点C的坐标;
(3)易得AC、AD的长,由于△ACD是直角三角形,那么AC•AD=AP•d1+AP•d2,由此可得d1+d2=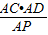 ,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤
,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤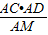 ,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.
,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.
解答:解:(1)解方程x2-4x+3=0得:
x=1或x=3,而OA<OB,
则点A的坐标为(-1,0),点B的坐标为(3,0);(1分)
∵A、B关于抛物线对称轴对称,
∴△DAB是等腰三角形,而∠DAB=45°,
∴△DAB是等腰直角三角形,得D(1,-2);
令抛物线对应的二次函数解析式为y=a(x-1)2-2,
∵抛物线过点A(-1,0),
∴0=4a-2,得a= ,
,
故抛物线对应的二次函数解析式为y= (x-1)2-2(或写成y=
(x-1)2-2(或写成y= x2-x-
x2-x- );(4分)
);(4分)
(2)∵CA⊥AD,∠DAC=90°,(5分)
又∵∠DAB=45°,
∴∠CAB=45°;
令点C的坐标为(m,n),则有m+1=n,(6分)
∵点C在抛物线上,
∴n= (m-1)2-2;(7分)
(m-1)2-2;(7分)
化简得m2-4m-5=0
解得m=5,m=-1(舍去),
故点C的坐标为(5,6);(8分)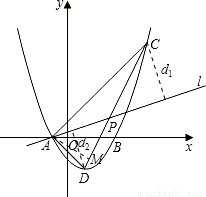
(3)由(2)知AC=6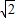 ,而AD=2
,而AD=2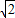 ,
,
∴DC= ;
;
过A作AM⊥CD,
又∵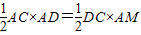 ,
,
∴AM=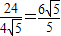 ,(9分)
,(9分)
又∵S△ADC=S△APD+S△APC
∴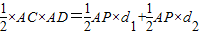 ,(11分)
,(11分)
d1+d2=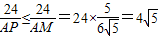 ;
;
即此时d1+d2的最大值为4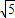 .(12分)
.(12分)
点评:此题主要考查了等腰直角三角形的性质、二次函数解析式的确定、函数图象交点坐标的求法、三角形面积的计算方法以及不等式的应用等重要知识,涉及知识面广,难度较大.
(2)由于AC⊥AD,且∠DAB=45°,则∠CAB=45°,设出点C的横坐标,那么其纵坐标应为m+1,然后将C点坐标代入抛物线的解析式中,即可求得点C的坐标;
(3)易得AC、AD的长,由于△ACD是直角三角形,那么AC•AD=AP•d1+AP•d2,由此可得d1+d2=
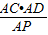 ,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤
,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤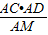 ,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.
,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.解答:解:(1)解方程x2-4x+3=0得:
x=1或x=3,而OA<OB,
则点A的坐标为(-1,0),点B的坐标为(3,0);(1分)
∵A、B关于抛物线对称轴对称,
∴△DAB是等腰三角形,而∠DAB=45°,
∴△DAB是等腰直角三角形,得D(1,-2);
令抛物线对应的二次函数解析式为y=a(x-1)2-2,
∵抛物线过点A(-1,0),
∴0=4a-2,得a=
 ,
,故抛物线对应的二次函数解析式为y=
 (x-1)2-2(或写成y=
(x-1)2-2(或写成y= x2-x-
x2-x- );(4分)
);(4分)(2)∵CA⊥AD,∠DAC=90°,(5分)
又∵∠DAB=45°,
∴∠CAB=45°;
令点C的坐标为(m,n),则有m+1=n,(6分)
∵点C在抛物线上,
∴n=
 (m-1)2-2;(7分)
(m-1)2-2;(7分)化简得m2-4m-5=0
解得m=5,m=-1(舍去),
故点C的坐标为(5,6);(8分)

(3)由(2)知AC=6
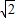 ,而AD=2
,而AD=2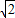 ,
,∴DC=
 ;
;过A作AM⊥CD,
又∵
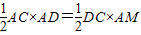 ,
,∴AM=
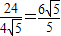 ,(9分)
,(9分)又∵S△ADC=S△APD+S△APC
∴
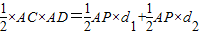 ,(11分)
,(11分)d1+d2=
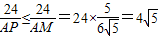 ;
;即此时d1+d2的最大值为4
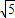 .(12分)
.(12分)点评:此题主要考查了等腰直角三角形的性质、二次函数解析式的确定、函数图象交点坐标的求法、三角形面积的计算方法以及不等式的应用等重要知识,涉及知识面广,难度较大.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.

 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.