题目内容
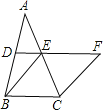
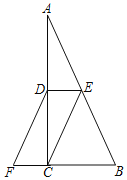
【题目】如图,在△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.
(1)求证:四边形DECF是平行四边形;
(2)若∠A=30°,写出图中所有与FD长度相等的线段.
【答案】(1)见解析;(2)AE=EB=BC=EC=DF
【解析】
(1)首先利用三角形中位线的性质得出DE∥BC,进而结合直角三角形的性质得出CE=![]() AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
AB=AE,得出∠CDF=∠ACE,推出DF∥CE,再利用平行四边形的定义判定即可.
(2)只要证明△EBC是等边三角形即可判定;
(1)证明:∵D,E分别为AC,AB的中点,
∴DE为△ACB的中位线,
∴DE//BC.
∵CE为Rt△ACB的斜边上的中线,
∴CE=![]() AB=AE.
AB=AE.
∴∠A=∠ACE.
又∵∠CDF=∠A,
∴∠CDF=∠ACE.
∴DF//CE.
又∵DE//BC,
∴四边形DECF为平行四边形.
(2)解:图中所有与FD长度相等的线段有:AE、BE、CE、BC;理由如下:
∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∵EC=EA=EB,
∴△EBC是等边三角形,
∴AE=EB=BC=EC=DF.

练习册系列答案
相关题目