题目内容
如图1,已知抛物线经过原点O和x轴上另一点D,顶点的坐标为(2,4),Rt△ABC的顶点A与点O重合,AC、AB分别在x轴、y轴上,且AC =3,AB =4。
(1)直线BC的解析式为 。
(2)求该抛物线的解析式。
(3)如图2,将Rt△ABC以每秒1个单位长度的速度沿x轴的正方向平行移动,同时一动点P也以相同的速度从点A出发向点B移动,设它们运动的时间为t秒(0≤t≤2),AB边与该抛物线的交点为Q。
①连接CP、CQ,设△CPQ的面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由。
②直接写出当直线BC与抛物线有唯一的公共点时t的值。
(1)直线BC的解析式为 。
(2)求该抛物线的解析式。
(3)如图2,将Rt△ABC以每秒1个单位长度的速度沿x轴的正方向平行移动,同时一动点P也以相同的速度从点A出发向点B移动,设它们运动的时间为t秒(0≤t≤2),AB边与该抛物线的交点为Q。
①连接CP、CQ,设△CPQ的面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由。
②直接写出当直线BC与抛物线有唯一的公共点时t的值。

解:(1) y=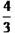 x+4
x+4
(2) ∵该抛物线的顶点的坐标为(2,4),
∴设该抛物线的解析式为y=a(x-2)2+4
又∵抛物线过原点,
∴a= -1
∴该抛物线的解析式为y=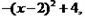 即y=
即y=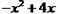 .
.
(3)①存在.
由题意,点P的坐标是(t,t),点Q的坐标是(t,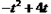 ),
),
∴PQ=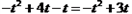 .
.
∴S=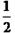 PQ
PQ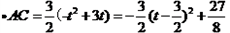 ,
,
∴当t=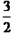 时,S存在最大值,最大值是
时,S存在最大值,最大值是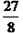 .
.
②当t=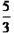 时,直线BC与抛物线有唯一的公共点.
时,直线BC与抛物线有唯一的公共点.
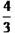 x+4
x+4 (2) ∵该抛物线的顶点的坐标为(2,4),
∴设该抛物线的解析式为y=a(x-2)2+4
又∵抛物线过原点,
∴a= -1
∴该抛物线的解析式为y=
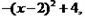 即y=
即y=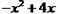 .
. (3)①存在.
由题意,点P的坐标是(t,t),点Q的坐标是(t,
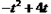 ),
), ∴PQ=
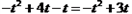 .
. ∴S=
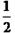 PQ
PQ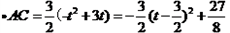 ,
, ∴当t=
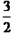 时,S存在最大值,最大值是
时,S存在最大值,最大值是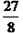 .
. ②当t=
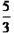 时,直线BC与抛物线有唯一的公共点.
时,直线BC与抛物线有唯一的公共点. 
练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克. 探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=
探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC= 已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克. 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经 ),点M是抛物线C2:
),点M是抛物线C2: (
( <0)的顶点.
<0)的顶点.
