题目内容
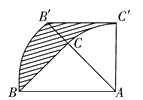
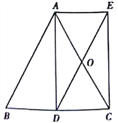
【题目】在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,……,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥1,且n为正整数).
(1)直接写出下列点B1B2,B3的坐标;
(2)写出抛物线L2,L3的解析式,并写出其中一个解析式的求解过程,再猜想抛物线Ln的顶点坐标;
(3)①设A1D1=k1·D1B1,A2D2=k2·D2B2,试判断k1与k2的数量关系并说明理由;
②点D1,D2,…,Dn是否在一条直线上?若是,直接写出这条直线与直线y=x+1的交点坐标;若不是,请说明理由.

【答案】(1)B1(1,1),B2(3,2),B3(7,4);(2)抛物线L2,L3的解析式分别为y=-(x-2)2+3,y=-![]() (x-5)2,求解过程见解析;猜想抛物线Ln的顶点坐标为(3×2n-2-1,3×2n-2); (3)①k1与k2的数量关系为k1=k2.理由见解析;②这条直线与直线y=x+1的交点坐标为(-1,0).
(x-5)2,求解过程见解析;猜想抛物线Ln的顶点坐标为(3×2n-2-1,3×2n-2); (3)①k1与k2的数量关系为k1=k2.理由见解析;②这条直线与直线y=x+1的交点坐标为(-1,0).
【解析】
(1)先求出直线y=x+1与y轴的交点坐标即可得出A1的坐标,故可得出OA1的长,根据四边形A1B1C1O是正方形即可得出B1的坐标,再把B1的横坐标代入直线y=x+1即可得出A1的坐标,同理可得出B2,B3的坐标;
(2)根据四边形A1B1C1O是正方形得出C1的坐标,再由点A2在直线y=x+1上可知A2(1,2),B2的坐标为(3,2),由抛物线L2的对称轴为直线x=2可知抛物线L2的顶点为(2,3),再用待定系数法求出直线L2的解析式;根据B3的坐标为(7,3),同上可求得点A3的坐标为(3,4),抛物线L3的对称轴为直线x=5,同理可得出直线L2的解析式;
(3)①同(2)可求得L2的解析式为y=(x-2)2+3,当y=1时,求出x的值,由A1D1=![]() -D1B1,可得出k1的值,同理可得出k2的值,由此可得出结论;
-D1B1,可得出k1的值,同理可得出k2的值,由此可得出结论;
②由①中的结论可知点D1、D2、…,Dn是否在一条直线上,再用待定系数法求出直线D1D2的解析式,求出与直线y=x+1的交点坐标即可.
(1) )∵令x=0,则y=1,
∴A1(0,1),
∴OA1=1.
∵四边形A1B1C1O是正方形,
∴A1B1=1,
∴B1(1,1).
∵当x=1时,y=1+1=2,
∴B2(3,2);
同理可得,B3(7,4).
故答案为:B1(1,1),B2(3,2),B3(7,4).
(2)抛物线L2,L3的解析式分别为y=-(x-2)2+3,y=-![]() (x-5)2+6.
(x-5)2+6.
抛物线L2的解析式的求解过程:
对于直线y=x+1,设x=0,可得y=1,
即A1(0,1).
∵A1B1C1O是正方形,
∴C1(1,0).
又∵点A2在直线y=x+1上,
∴点A2(1,2).
又∵点B2的坐标为(3,2),
∴抛物线L2的对称轴为直线x=2.
∴抛物线L2的顶点坐标为(2,3).
设抛物线L2的解析式为y=a(x-2)2+3(a≠0),
∵L2过点B2(3,2),
∴当x=3时,y=2,即2=a×(3-2)2+3,解得a=-1.
∴抛物线L2的解析式为y=-(x-2)2+3.
(或抛物线L3的解析式的求解过程:
∵B3的坐标为(7,4),同上可求得点A3的坐标为(3,4),
∴抛物线L3的对称轴为直线x=5.
∴抛物线L3的顶点坐标为(5,6).
设抛物线L3的解析式为y=a(x-5)2+6(a≠0),
∵L3过点B3(7,4),
∴当x=7时,y=4,即4=a×(7-5)2+6,解得a=-![]() .
.
∴抛物线L3的解析式为y=-![]() (x-5)2+6.)
(x-5)2+6.)
猜想抛物线Ln的顶点坐标为(3×2n-2-1,3×2n-2);
猜想过程:方法1:可由抛物线L1,L2,L3…的解析式:
y=-2![]() ,y=-(x-2)2+3,y=-
,y=-(x-2)2+3,y=-![]() (x-5)2+6,……,归纳总结得出.
(x-5)2+6,……,归纳总结得出.
方法2:可由正方形AnBnCnCn-1顶点An,Bn的坐标规律An(2n-1-1,2n-1)与Bn(2n-1,2n-1),
再利用对称性可得抛物线Ln的对称轴为直线x=![]() ,即x=
,即x=![]() =3·2n-2-1,
=3·2n-2-1,
又顶点在直线y=x+1上,所以可得抛物线Ln的顶点坐标为(3×2n-2-1,3×2n-2).
(3)①k1与k2的数量关系为k1=k2.
理由如下:由(2)可知L2的解析式为y=-(x-2)2+3,
当y=1时,1=-(x-2)2+3,解得x1=2-![]() ,x2=2+
,x2=2+![]() .
.
∵0<A1D1<1,所以x=2-![]() .
.
∴A1D1=2-![]() -1).
-1).
∴D1B1=1-(2-![]() )=
)=![]() -1.
-1.
∴A1D1=![]() ·D1B1,即k1=
·D1B1,即k1=![]() .
.
同理可求得A2D2=4-2![]() =2
=2![]() -1),
-1),
D2B2=2-(4-2![]() )=2
)=2![]() -2=2(
-2=2(![]() -1),
-1),
A2D2=![]() ·D2B2,即k2=
·D2B2,即k2=![]() ,
,
∴k1=k2.
②点D1,D2,…,Dn是在一条直线上.
这条直线与直线y=x+1的交点坐标为(-1,0).

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案