题目内容
梯形的高为12,两条对角线的长分别为15,20,则此梯形的面积为________.
150
分析:根据题意作图,分别利用勾股定理求得BF,CE的长,从而可得到上下底的和,根据梯形的面积公式计算即可.
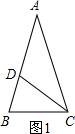
解答: 解:作梯形的高AE,DF,如图1,
解:作梯形的高AE,DF,如图1,
在直角三角形BDF中,利用勾股定理可求出BF=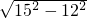 =9,
=9,
在直角三角形ACE中,利用勾股定理可求出CE=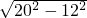 =16,
=16,
∴CE+BF=25=BC+EF
∵EF=AD
∴BC+AD=25
∴梯形的面积=25×12÷2=150.
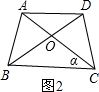
②作梯形的高AE,DF,F在BC的延长线上,如图2:
在直角三角形BDF中,利用勾股定理可求出BF=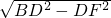 =
=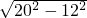 =16,
=16,
在直角三角形ACE中,利用勾股定理可求出CE=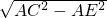 =
=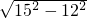 =9,
=9,
∴AD+BC=BC+EF=BF+EC=25,
∴梯形的面积= (AD+BC)×AE=
(AD+BC)×AE= (BF-EC)×AE=
(BF-EC)×AE= ×25×12=150.
×25×12=150.
综上可得梯形的面积为:150.
点评:本题的基本公式是梯形的面积,但要求梯形的面积就要有上底和下底的长,所以此题的关键之外是利用勾股定理求出上底和下底的长.
分析:根据题意作图,分别利用勾股定理求得BF,CE的长,从而可得到上下底的和,根据梯形的面积公式计算即可.
解答:
 解:作梯形的高AE,DF,如图1,
解:作梯形的高AE,DF,如图1,在直角三角形BDF中,利用勾股定理可求出BF=
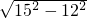 =9,
=9,在直角三角形ACE中,利用勾股定理可求出CE=
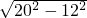 =16,
=16,∴CE+BF=25=BC+EF
∵EF=AD
∴BC+AD=25
∴梯形的面积=25×12÷2=150.
②作梯形的高AE,DF,F在BC的延长线上,如图2:
在直角三角形BDF中,利用勾股定理可求出BF=
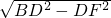 =
=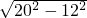 =16,
=16,在直角三角形ACE中,利用勾股定理可求出CE=
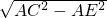 =
=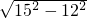 =9,
=9,∴AD+BC=BC+EF=BF+EC=25,
∴梯形的面积=
 (AD+BC)×AE=
(AD+BC)×AE= (BF-EC)×AE=
(BF-EC)×AE= ×25×12=150.
×25×12=150.综上可得梯形的面积为:150.
点评:本题的基本公式是梯形的面积,但要求梯形的面积就要有上底和下底的长,所以此题的关键之外是利用勾股定理求出上底和下底的长.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
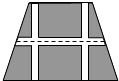 如图,要设计一个等腰梯形的花坛,花坛上底长12米,下底长18米,高8米.
如图,要设计一个等腰梯形的花坛,花坛上底长12米,下底长18米,高8米.