题目内容
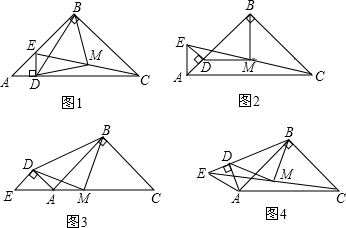
如图①,已知点D在AC上,△ABC和△ADE都是等腰直角三角形,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)将图①中的△ADE绕点A逆时针旋转45°,如图②所示,则(1)题中的结论“△BMD为等腰直角三角形”是否仍然成立?请说明理由.

(1)证明:∵点M是Rt△BEC的斜边EC的中点,
∴BM= EC=MC,
EC=MC,
∴∠MBC=∠MCB.
∴∠BME=2∠BCM.
同理可证:DM= EC=MC,∠EMD=2∠MCD.
EC=MC,∠EMD=2∠MCD.
∴∠BMD=2∠BCA=90°,
∴BM=DM.
∴△BMD是等腰直角三角形.
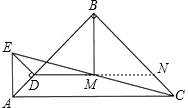
(2)(1)题中的结论仍然成立.
理由:延长DM与BC交于点N,
∵DE⊥AB,CB⊥AB,
∴∠EDB=∠CBD=90°,
∴DE∥BC.
∴∠DEM=∠MCN.
又∵∠EMD=∠NMC,EM=MC,
∴△EDM≌△MNC.
∴DM=MN.DE=NC=AD.
又AB=BC,
∴AB-AD=BC-CN,
∴BD=BN.
∴BM⊥DM.即∠BMD=90°.
∵∠ABC=90°,
∴BM= DN=DM.
DN=DM.
∴△BMD是等腰直角三角形.
分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出BM=EN=MC,DM=EM=MC,然后根据等边对等角的性质可以证明∠BMD=90°,所以△BMD为等腰直角三角形;
(2)延长DM交BC于N,先根据∠EDB=∠ABC=90°证明ED∥BC,然后根据两直线平行,内错角相等求出∠DEM=∠MCN,从而证明△EDM与△MNC全等,根据全等三角形对应边相等可得DM=MN,然后即可证明BM⊥DM,且BM=DM.
点评:本题主要考查了全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握判定定理及性质并灵活运用是解题的关键,难度中等.
∴BM=
 EC=MC,
EC=MC,∴∠MBC=∠MCB.
∴∠BME=2∠BCM.
同理可证:DM=
 EC=MC,∠EMD=2∠MCD.
EC=MC,∠EMD=2∠MCD.∴∠BMD=2∠BCA=90°,
∴BM=DM.
∴△BMD是等腰直角三角形.

(2)(1)题中的结论仍然成立.
理由:延长DM与BC交于点N,
∵DE⊥AB,CB⊥AB,
∴∠EDB=∠CBD=90°,
∴DE∥BC.
∴∠DEM=∠MCN.
又∵∠EMD=∠NMC,EM=MC,
∴△EDM≌△MNC.
∴DM=MN.DE=NC=AD.
又AB=BC,
∴AB-AD=BC-CN,
∴BD=BN.
∴BM⊥DM.即∠BMD=90°.
∵∠ABC=90°,
∴BM=
 DN=DM.
DN=DM.∴△BMD是等腰直角三角形.
分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出BM=EN=MC,DM=EM=MC,然后根据等边对等角的性质可以证明∠BMD=90°,所以△BMD为等腰直角三角形;
(2)延长DM交BC于N,先根据∠EDB=∠ABC=90°证明ED∥BC,然后根据两直线平行,内错角相等求出∠DEM=∠MCN,从而证明△EDM与△MNC全等,根据全等三角形对应边相等可得DM=MN,然后即可证明BM⊥DM,且BM=DM.
点评:本题主要考查了全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握判定定理及性质并灵活运用是解题的关键,难度中等.

练习册系列答案
相关题目