题目内容
(2011•资阳)在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒.
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
(参考数据:
≈1.414,
≈1.732,
≈2.236,
≈2.449)

(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
(参考数据:
| 2 |
| 3 |
| 5 |
| 6 |
分析:(1)根据已知先求出沿A→O→B路线行进所用时间,然后由勾股定理求出AB,从而求出沿A→B路线行进所用时间;
(2)首先解Rt△OBC,运用三角函数求出BC,继而得出AC,从而求出沿A→C→B路线到达B处所用的时间;
(3)在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,分别求出沿A→P→B路线行进所用时间和沿A→P′→B路线行进所用时间进行比较得出结论.
(2)首先解Rt△OBC,运用三角函数求出BC,继而得出AC,从而求出沿A→C→B路线到达B处所用的时间;
(3)在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,分别求出沿A→P→B路线行进所用时间和沿A→P′→B路线行进所用时间进行比较得出结论.
解答:解:(1)沿A→O→B路线行进所用时间为:600÷20+300÷10=60(秒),(1分)
在Rt△OBA中,由勾股定理,得AB=
=300
(cm).(2分)
∴沿A→B路线行进所用时间为:300
÷10≈300×2.236÷10≈67(秒).(3分)
(2)在Rt△OBC中,OB=300,∠OCB=45°,∴OC=OB=300cm,BC=
=300
(cm)(4分)
∴AC=600-300=300(cm).
∴沿A→C→B路线行进所用时间为:AC÷20+BC÷10=300÷20+300
÷10≈15+42.42≈57(秒).
(3)在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,
在Rt△APE和Rt△AP′E′中,sin30°=
=
,∴EP=
,E′P′=
.(7分)
∴沿A→P→B路线行进所用时间为:AP÷20+PB÷10=EP÷10+PB÷10=(EP+PB)÷10=
BE(秒),
沿A→P′→B路线行进所用时间为:
AP′÷20+P′B÷10=E′P′÷10+P′B÷10=(E′P′+P′B)÷10=
(E′P′+P′B)(秒).(8分)
连接BE′,则E′P′+P′B>BE′>BE,∴
BE<
(E′P′+P′B).
∴沿A→P→B路线行进所用时间,小于沿A→P′→B路线行进所用时间.
即机器人沿A→P→B路线行进所用时间最短.(9分)
在Rt△OBA中,由勾股定理,得AB=
| 6002+3002 |
| 5 |
∴沿A→B路线行进所用时间为:300
| 5 |
(2)在Rt△OBC中,OB=300,∠OCB=45°,∴OC=OB=300cm,BC=
| 300 |
| sin45° |
| 2 |
∴AC=600-300=300(cm).
∴沿A→C→B路线行进所用时间为:AC÷20+BC÷10=300÷20+300
| 2 |
(3)在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,
在Rt△APE和Rt△AP′E′中,sin30°=
| EP |
| AP |
| E′P′ |
| AP′ |
| AP |
| 2 |
| AP′ |
| 2 |
∴沿A→P→B路线行进所用时间为:AP÷20+PB÷10=EP÷10+PB÷10=(EP+PB)÷10=
| 1 |
| 10 |
沿A→P′→B路线行进所用时间为:
AP′÷20+P′B÷10=E′P′÷10+P′B÷10=(E′P′+P′B)÷10=
| 1 |
| 10 |
连接BE′,则E′P′+P′B>BE′>BE,∴
| 1 |
| 10 |
| 1 |
| 10 |
∴沿A→P→B路线行进所用时间,小于沿A→P′→B路线行进所用时间.
即机器人沿A→P→B路线行进所用时间最短.(9分)
点评:此题考查的知识点是解直角三角形的应用,关键是运用三角函数和勾股定理求出路线长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
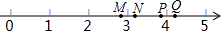 (2011•资阳)如图,在数轴上表示实数
(2011•资阳)如图,在数轴上表示实数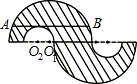
 (2011•资阳)在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款
(2011•资阳)在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款 (2011•资阳)如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
(2011•资阳)如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.