Question

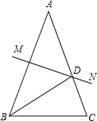
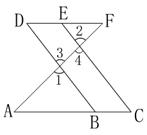
如图，点E是DF上一点，点B在AC上，∠1=∠2，∠C=∠D，试说明DF∥AC的理由。

理由：∵∠1=∠2 （已知）
∠1=∠3，∠2=∠4 （                  ）
∴∠3=∠4 (                  )
∴______∥______ （                              ）
∴∠C=∠DBA （                              ）
又∵∠C=∠D （ 已知 ）
∴∠DBA=∠D （                     ）
∴DF∥AC （                               ）

Answer 1

对顶角相等；等量代换；内错角相等，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行

试题分析：根据平行线的判定与性质依次分析即可得到结果.
理由：∵∠1=∠2 （已知）
∠1=∠3，∠2=∠4 （对顶角相等）
∴∠3=∠4 (等量代换)
∴BD∥CE（内错角相等，两直线平行）
∴∠C=∠DBA （两直线平行，同位角相等）
又∵∠C=∠D （ 已知 ）
∴∠DBA=∠D （等量代换)
∴DF∥AC （内错角相等，两直线平行）.
点评：平行线的判定与性质是初中数学的重点，贯穿于整个初中数学的学习，是中考常见题，一般难度不大，需熟练掌握.