题目内容
如图:点P是边长为1的正方形内(不在边上)任意一点,P和正方形各顶点相连后把正方形分成4块,其中①③可以重新拼成一个四边形,重拼后的四边形周长的最小值是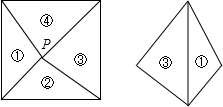
2
| 2 |
2
.| 2 |

分析:根据题意得出P点在正方形对角线上时,重拼后的四边形周长的最小值进而求出即可.
解答:解:∵①③可以重新拼成一个四边形,重拼后的四边形周长为:P点到正方形4个顶点的距离之和,
∴重拼后的四边形周长的最小值时,结合三角形三边关系,则P点在正方形对角线上,
∴重拼后的四边形周长的最小值是:2
=2
.
故答案为:2
.
∴重拼后的四边形周长的最小值时,结合三角形三边关系,则P点在正方形对角线上,
∴重拼后的四边形周长的最小值是:2
| 12+12 |
| 2 |
故答案为:2
| 2 |
点评:此题主要考查了正方形的性质以及勾股定理等知识,根据已知得出P点位置是解题关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
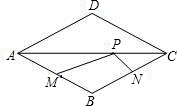 如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )
如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )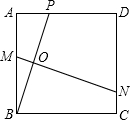 垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.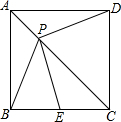 如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB
如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB 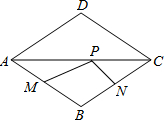 如图,点P是边长为1的菱形ABCD的对角线AC上一动点,点M、N分别是AB、BC中点,求MP+NP的最小值.
如图,点P是边长为1的菱形ABCD的对角线AC上一动点,点M、N分别是AB、BC中点,求MP+NP的最小值.