题目内容
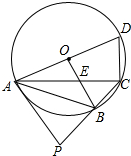 (2012•天水)如图,四边形ABCD内接于⊙O,已知直径AD=6,∠ABC=120°,∠ACB=45°,连接OB交AC于点E.
(2012•天水)如图,四边形ABCD内接于⊙O,已知直径AD=6,∠ABC=120°,∠ACB=45°,连接OB交AC于点E.(1)求AC的长.
(2)求CE:EA的值.
(3)在CB的延长线上取一点P,使CB=
| 1 | 2 |
分析:(1)利用圆周角定理和“圆内接四边形的对角互补”的性质推知△ACD是直角三角形,且∠D=60°,所以通过解该直角三角形来求AC的长度即可;
(2)利用圆周角定理推知∠AOB=90°.所以在Rt△AOB中求得EA=2
.结合(1)中AC=3
即可求得CE的值;
(3)欲证直线PA与⊙O相切,只需证明AD⊥AP即可.
(2)利用圆周角定理推知∠AOB=90°.所以在Rt△AOB中求得EA=2
| 3 |
| 3 |
(3)欲证直线PA与⊙O相切,只需证明AD⊥AP即可.
解答:解:(1)∵∠ABC=120°,∴∠D=60°.
∵AD是⊙O的直径,∴∠ACD=90°.
∵AD=6,∴AC=AD•sin60°=6×
=3
.
(2)∵∠ACB=45°,∴∠AOB=2∠ACB=90°.
∴EA=
=2
.∴CE=AC-AE=
.
∴CE:EA=
:2
=1:2.
(3)证明:∵
=
,
=
,
∴
=
.
∴BE∥AP.
∵∠AOB=90°,
∴PA⊥OA.
∴直线PA与⊙O相切.
∵AD是⊙O的直径,∴∠ACD=90°.
∵AD=6,∴AC=AD•sin60°=6×
| ||
| 2 |
| 3 |
(2)∵∠ACB=45°,∴∠AOB=2∠ACB=90°.
∴EA=
| OA |
| cos30° |
| 3 |
| 3 |
∴CE:EA=
| 3 |
| 3 |
(3)证明:∵
| CB |
| BP |
| 1 |
| 2 |
| CE |
| EA |
| 1 |
| 2 |
∴
| CB |
| BP |
| CE |
| EA |
∴BE∥AP.
∵∠AOB=90°,
∴PA⊥OA.
∴直线PA与⊙O相切.
点评:本题综合考查了圆周角定理,切线的判定与性质以及解直角三角形.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
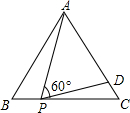 (2012•天水)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为
(2012•天水)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为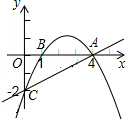 (2012•天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(2012•天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.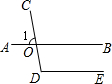 (2012•天水)如图,已知直线AB、CD相交于点O,∠1=80°,如果DE∥AB,那么∠D的度数是( )
(2012•天水)如图,已知直线AB、CD相交于点O,∠1=80°,如果DE∥AB,那么∠D的度数是( ) (2012•天水)如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE.
(2012•天水)如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于点E,交BC边于点F,交AC于点O,分别连接AF和CE.