题目内容
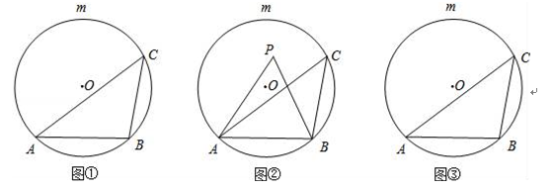
【题目】如图①,AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)若∠ACB=45°,点P是⊙O上一点(不与A、B重合),则∠APB= ;
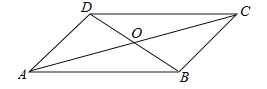
(2)如图②,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
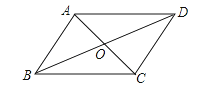
(3)请在图③中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
【答案】(1)45°或135°;(2)∠APB>∠ACB;(3)图见解析
【解析】
试题分析:(1)根据题意可知,存在两种情况,针对两种情况,可以画出相应的图形,由题目中的信息和同弧所对的圆周角相等,圆内接四边形对角互补,可以分别求得两种情况下∠APB的度数,本题得以解决;
(2)根据题意画出相应的图形,根据三角形的外角大于任何一个和它不相邻的内角,可以证明结论成立,本题得以解决;
(3)根据题意和第(2)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决.
试题解析:(1)解:如图①所示,
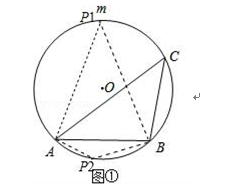
根据题意可分两种情况,
第一种情况,当点P在P1时,
可知,∠AP1B=∠ACB=45°;
第二种情况,当点P在P2时,
∵四边形ACBP2是圆内接四边形,
∴∠AP2B+∠ACB=180°,
∵∠ACB=45°,
∴∠AP2B=135°,
故答案为:45°或135°;
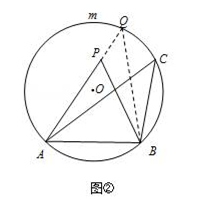
(2)证明:如下图②所示,延长AP交⊙O于点Q,连接BQ.
则∠PQB=∠ACB,
∵∠APB为△PQB的一个外角,
∴∠APB>∠PQB,
即∠APB>∠ACB;
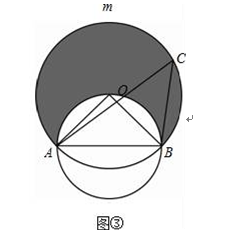
(3)点P所在的范围如下图③所示,

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目