题目内容
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

【答案】(1)证明见解析;(2)EG=![]() AG﹣BG,理由见解析.
AG﹣BG,理由见解析.
【解析】试题分析:(1)如图,作∠GAH=∠EAB交GE于点H,易证△ABG≌△AEH ,再判定△AGH是等边三角形,即可得结论;(2)EG=![]() AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
试题解析:
如图,作∠GAH=∠EAB交GE于点H
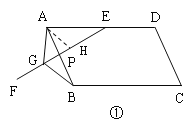
∴∠GAB=∠HAE
∵∠EAB =∠EGB,∠APE=∠BPG
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=60°
∴△AGH是等边三角形
∴AG=GH
∴EG=AG+BG
(2) EG=![]() AG-BG,
AG-BG,
如图②,作∠GAH=∠EAB交GE于点H
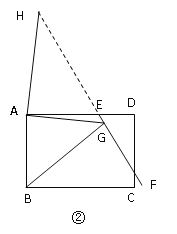
∴∠GAB=∠HAE
又∵∠EGB=∠EAB=90°
∴∠ABG+∠AEG=∠AEG+∠AEH=180°
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
又∵∠GAH =∠EAB=90°
∴△AGH是等腰直角三角形
∴![]() AG=HG
AG=HG
∴EG=![]() AG-BG
AG-BG

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】未成年人思想道德建设越来越受到社会的关注,辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成了频
分组 | 频数 | 频率 |
0.5~50.5 |
| 0.1 |
50.5~ | 20 | 0.2 |
100.5~150.5 |
|
|
200.5 | 30 | 0.3 |
200.5~250.5 | 10 | 0.1 |
率分布表和频率分布直方图(如图).
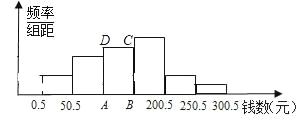
(1)补全频率分布表;
(2)在频率分布直方图中,长方形ABCD的面积是 ;这次调查的样本容量是 ;
(3)研究所认为,应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议.