题目内容
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”
(1)已知:如图,在△ABC中,∠C=90°,BC=2
,AB=2
.求证:△ABC是“匀称三角形”;
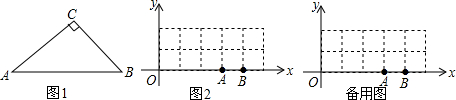
(2)在平面直角坐标系xOy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图,现有10个边长是1的小正方形组成的长方形区域记为G,每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧.在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
(1)已知:如图,在△ABC中,∠C=90°,BC=2
| 3 |
| 7 |

(2)在平面直角坐标系xOy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图,现有10个边长是1的小正方形组成的长方形区域记为G,每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧.在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
下列说法:
(1)矩形的对角线相互垂直且平分;
(2)菱形的四边相等;
(3)一组对边平行,另一组对边相等的四边形是平行四边形;
(4)正方形的对角线相等,并且互相垂直平分;
(5)顺次连接平行四边形各边中点所得到的四边形是矩形.
其中正确的个数是( )
(1)矩形的对角线相互垂直且平分;
(2)菱形的四边相等;
(3)一组对边平行,另一组对边相等的四边形是平行四边形;
(4)正方形的对角线相等,并且互相垂直平分;
(5)顺次连接平行四边形各边中点所得到的四边形是矩形.
其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
如果正n边形的每一个内角都等于144°,那么n等于( )
| A、9 | B、10 | C、11 | D、12 |
若∠A=45°18′,∠B=45°15′30″,∠C=45.15°,则( )
| A、∠A>∠B>∠C | B、∠B>∠A>∠C | C、∠A>∠C>∠B | D、∠C>∠A>∠B |
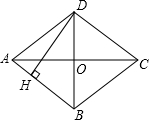 如图,在菱形ABCD中,AC=2
如图,在菱形ABCD中,AC=2| 3 |
A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
10月份,我校初2014级全体学生举行了实心球测试,下面是某组(6名)男同学的测试成绩(单位:米):7.6,8.8,8.6,9.5,8.4,8.8,则该组数据的众数、中位数分别为( )
| A、8.6,8.7 | B、8.8,8.6 | C、8.8,8.7 | D、8.8,8.8 |

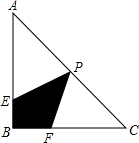 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P为AC中点,E为AB边上一动点,F为BC边上一动点,且满足条件∠EPF=45°,记四边形PEBF的面积为S1;