题目内容
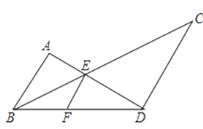
【题目】如图，F在BD上，BC、AD相交于点E，且AB∥CD∥EF，
（1）图中有哪几对位似三角形，选其中一对加以证明；
（2）若AB=2，CD=3，求EF的长．
【答案】（1）一共有3对；
（2）EF=
．
【解析】
试题（1）利用相似三角形的判定方法以及位似图形的性质进而得出答案；
（2）利用比例的性质以及相似三角形的性质进而求出
=
=
，求出EF即可
试题解析：（1）∵AB∥CD∥EF，
∴△DFE∽△DBA，△BFE∽△BDC，△AEB∽△DEC，
且对应边都交于一点，
∴△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形，
一共有3对；
（2）∵△BFE∽△BDC，△AEB∽△DEC，AB=2，CD=3，
∴
=
=
，
∴
=
=
，
∴解得：EF=．
练习册系列答案
相关题目
【题目】小明同学三次到某超市购买A、B两种商品，其中仅有一次是有折扣的，购买数量及消费金额如下表：
类别 次数 | 购买A商品数量（件） | 购买B商品数量（件） | 消费金额（元） |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题：
（1）第 次购买有折扣；
（2）求A、B两种商品的原价；
（3）若购买A、B两种商品的折扣数相同，求折扣数；
（4）小明同学再次购买A、B两种商品共10件，在（3）中折扣数的前提下，消费金额不超过200元，求至少购买A商品多少件．
