ƒøƒ⁄»ð
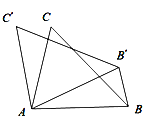
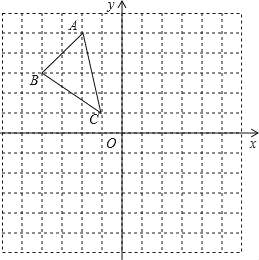
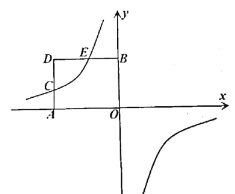
°æƒø°ø»ÁÕº£¨∂•µ„Œ™P£®2£¨©Å4£©µƒ∂˛¥Œ∫Ø ˝y£Ωax2+bx+cµƒÕºœÛæ≠π˝‘≠µ„£¨µ„A£®m£¨n£©‘⁄∏√∫Ø ˝ÕºœÛ…œ£¨¡¨Ω”AP°¢OP£Æ
£®1£©«Û∂˛¥Œ∫Ø ˝y£Ωax2+bx+cµƒ±Ì¥Ô Ω£ª
£®2£©»Ù°œAPO£Ω90°„£¨«Ûµ„Aµƒ◊¯±Í£ª
£®3£©»Ùµ„Aπÿ”⁄≈◊ŒÔœþµƒ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™C£¨µ„Aπÿ”⁄y÷·µƒ∂‘≥∆µ„Œ™D£¨…Ë≈◊ŒÔœþ”Îx÷·µƒ¡Ì“ªΩªµ„Œ™B£¨«ÎΩ‚¥œ¬¡–Œ £∫
¢Ÿµ±m°Ÿ4 ±£¨ ‘≈–∂œÀƒ±þ–ŒOBCDµƒ–Œ◊¥≤¢Àµ√˜¿Ì”…£ª
¢⁄µ±n£º0 ±£¨»ÙÀƒ±þ–ŒOBCDµƒ√ʪ˝Œ™12£¨«Ûµ„Aµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©y£Ωx2©Å4x£ª£®2£©A£®![]() £¨©Å
£¨©Å![]() £©£ª£®3£©¢Ÿ∆Ω––Àƒ±þ–Œ£¨¿Ì”…º˚Ω‚Œˆ£ª¢⁄A£®1£¨©Å3£©ªÚA£®3£¨©Å3£©£Æ
£©£ª£®3£©¢Ÿ∆Ω––Àƒ±þ–Œ£¨¿Ì”…º˚Ω‚Œˆ£ª¢⁄A£®1£¨©Å3£©ªÚA£®3£¨©Å3£©£Æ
°æΩ‚Œˆ°ø
£®1£©”…“—÷™ø…µ√≈◊ŒÔœþ”Îx÷·¡Ì“ª∏ˆΩªµ„£®4£¨0£©£¨Ω´£®2£¨©Å4£©°¢£®4£¨0£©°¢£®0£¨0£©¥˙»Îy£Ωax2+bx+cº¥ø…«Û±Ì¥Ô Ω£ª
£®2£©”…°œAPO£Ω90°„£¨ø…÷™AP°ÕPO£¨À˘“‘m©Å2£Ω![]() £¨º¥ø…«ÛA£®
£¨º¥ø…«ÛA£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
£®3£©¢Ÿ”…“—÷™ø…µ√C£®4©Åm£¨n£©£¨D£®©Åm£¨n£©£¨B£®4£¨0£©£¨ø…µ√CD°ŒOB£¨CD£ΩCB£¨À˘“‘Àƒ±þ–ŒOBCD «∆Ω––Àƒ±þ–Œ£ª
¢⁄Àƒ±þ–Œ”…OBCD «∆Ω––Àƒ±þ–Œ£¨![]() £¨À˘“‘12£Ω4°¡£®©Ån£©£¨º¥ø…«Û≥ˆA£®1£¨©Å3£©ªÚA£®3£¨©Å3£©£Æ
£¨À˘“‘12£Ω4°¡£®©Ån£©£¨º¥ø…«Û≥ˆA£®1£¨©Å3£©ªÚA£®3£¨©Å3£©£Æ
Ω‚£∫£®1£©°þÕºœÛæ≠π˝‘≠µ„£¨
°ýc£Ω0£¨
°þ∂•µ„Œ™P£®2£¨©Å4£©
°ý≈◊ŒÔœþ”Îx÷·¡Ì“ª∏ˆΩªµ„£®4£¨0£©£¨
Ω´£®2£¨©Å4£©∫Õ£®4£¨0£©¥˙»Îy£Ωax2+bx£¨
°ýa£Ω1£¨b£Ω©Å4£¨
°ý∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™y£Ωx2©Å4x£ª
£®2£©°þ°œAPO£Ω90°„£¨
°ýAP°ÕPO£¨
°þA£®m£¨m2©Å4m£©£¨
°ým©Å2£Ω![]() £¨
£¨
°ým£Ω![]() £¨
£¨
°ýA£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
£®3£©¢Ÿ”…“—÷™ø…µ√C£®4©Åm£¨n£©£¨D£®©Åm£¨n£©£¨B£®4£¨0£©£¨
°ýCD°ŒOB£¨
°þCD£Ω4£¨OB£Ω4£¨
°ýÀƒ±þ–ŒOBCD «∆Ω––Àƒ±þ–Œ£ª
¢⁄°þÀƒ±þ–ŒOBCD «∆Ω––Àƒ±þ–Œ£¨![]() £¨
£¨
°ý12£Ω4°¡£®©Ån£©£¨
°ýn£Ω©Å3£¨
°ýA£®1£¨©Å3£©ªÚA£®3£¨©Å3£©£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°øº◊°¢““¡Ω√˚∂”‘±≤Œº”…‰ª˜—µ¡∑£¨√ø»À…‰ª˜10¥Œ£¨≥…º®∑÷±»Áœ¬£∫

∏˘æð“‘…œ–≈œ¢£¨’˚¿Ì∑÷Œˆ ˝æð»Áœ¬£∫
∆Ωæ˘≥…º®/ª∑ | ÷–Œª ˝/ª∑ | ÷⁄ ˝/ª∑ | ∑Ω≤Ó | |
º◊ | a | 7 | 7 | 1.2 |
““ | 7 | b | 8 | c |
£®1£©a£Ω_____£ªb£Ω_____£ªc£Ω_____£ª
£®2£©ÃÓø’£∫£®ÃÓ°∞º◊°±ªÚ°∞““°±£©£Æ
¢Ÿ¥”∆Ωæ˘ ˝∫Õ÷–Œª ˝µƒΩ«∂»¿¥±»Ωœ£¨≥…º®Ωœ∫√µƒ «_____£ª
¢⁄¥”∆Ωæ˘ ˝∫Õ÷⁄ ˝µƒΩ«∂»¿¥±»Ωœ£¨≥…º®Ωœ∫√µƒ «_____£ª
¢€≥…º®œý∂‘ΩœŒ»∂®µƒ «_____£Æ