题目内容
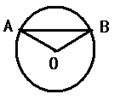
如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120°,求△AOB的面积.

100 cm2.
cm2.
 cm2.
cm2.试题分析:过O作OC垂直于AB,由垂径定理得到C为AB的中点,再利用等腰三角形的两底角相等,由∠AOB=120°,求出∠A为30°,在直角三角形AOC中,利用30°所对的直角边等于斜边的一半由OA的长求出OC的长,再利用勾股定理求出AC的长,由AB=2AC求出AB的长,利用三角形的面积公式即可求出三角形AOB的面积.
试题解析:如图,过O作OC⊥AB,交AB于点C,
则C为AB的中点,即AC=BC,
∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
在Rt△AOC中,OA=20cm,∠A=30°,
∴OC=
 OA=10cm,
OA=10cm,根据勾股定理得:AC2=OA2?OC2=300,
∴AB=2AC=20
 cm,
cm,则S△AOB=
 AB•OC=
AB•OC= ×20
×20 ×10=100
×10=100 cm2.
cm2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
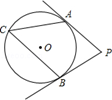
 上的一个动点,连结OP,并延长OP交线段BC于点K,过点P作⊙O的切线,分别交射线AB于点M,交直线BC于点G. 若
上的一个动点,连结OP,并延长OP交线段BC于点K,过点P作⊙O的切线,分别交射线AB于点M,交直线BC于点G. 若 ,则BK﹦ .
,则BK﹦ .




 的灰色扇形OAB,其中OA的长度 为6
的灰色扇形OAB,其中OA的长度 为6  ,且OA与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至点A再一次接触地面,如图(乙)所示,则O点移动了( )
,且OA与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至点A再一次接触地面,如图(乙)所示,则O点移动了( )

