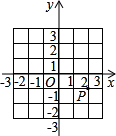题目内容
正整数集只是有理数集合的一部分,有趣的是,德国数学家康托尔(1845-1918)曾将所有有理数像正整数那样排列成一列纵队,从而和正整数集一一对应起来,让我们跟随康托尔的思路吧!
任何一个有理数都可以写成一个既约分数
(p是整数,q是正整数),它可以对应网格纸(如图)上的一个点,即p所在行与q所在列的交点,记为(q,p).如
对应图中的点A(3,1),这样,每个有理数对应着网格纸上的格点(水平线与竖直线的交叉点),而康托尔用图中的方法从中心O出发“螺旋式”地扩展开去,将平面内所有格点“一网打尽”.在图中,O(0,0)是第一个点,A(1,-1)是第______个点,B(-1,2)是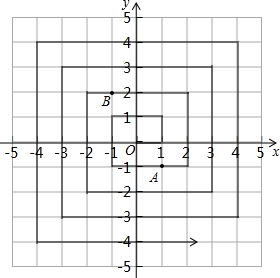 第______个点,第35个点是______.
第______个点,第35个点是______.
任何一个有理数都可以写成一个既约分数
| p |
| q |
| 1 |
| 3 |
 第______个点,第35个点是______.
第______个点,第35个点是______.O(0,0)是第一个点,A(1,-1)是第9个点,B(-1,2)是第16个点,第35个点是(-1,3).
故答案为9,16,(-1,3).
故答案为9,16,(-1,3).

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目