题目内容
 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA′B′C′的位置.若OB=4
如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA′B′C′的位置.若OB=4| 3 |
(-2
,2
)
| 6 |
| 6 |
(-2
,2
)
.| 6 |
| 6 |
分析:根据菱形的邻角互补求出∠AOC=60°,再根据菱形的对角线平分一组对角求出∠AOB=30°,过点B′作B′D⊥x轴于点D,然后求出∠B′OD=45°,再解直角三角形求出OD、B′D的长度,再根据点B′在第二象限解答.
解答: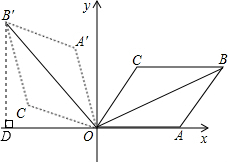 解:菱形OABC中,∵∠C=120°,
解:菱形OABC中,∵∠C=120°,
∴∠AOC=180°-120°=60°,
∴∠AOB=30°,
∵旋转角度数为105°,
∴∠BOB′=105°,
过点B′作B′D⊥x轴于点D,
则∠B′OD=180°-105°-30°=45°,
∵菱形OABC绕原点O逆时针旋转105°至OA′B′C′,
∴OB′=OB=4
,
∴OD=OB′cos45°=4
×
=2
,
B′D=OB′sin45°=4
×
=2
,
所以,点B′的坐标为(-2
,2
).
故答案为:(-2
,2
).
 解:菱形OABC中,∵∠C=120°,
解:菱形OABC中,∵∠C=120°,∴∠AOC=180°-120°=60°,
∴∠AOB=30°,
∵旋转角度数为105°,
∴∠BOB′=105°,
过点B′作B′D⊥x轴于点D,
则∠B′OD=180°-105°-30°=45°,
∵菱形OABC绕原点O逆时针旋转105°至OA′B′C′,
∴OB′=OB=4
| 3 |
∴OD=OB′cos45°=4
| 3 |
| ||
| 2 |
| 6 |
B′D=OB′sin45°=4
| 3 |
| ||
| 2 |
| 6 |
所以,点B′的坐标为(-2
| 6 |
| 6 |
故答案为:(-2
| 6 |
| 6 |
点评:本题考查了坐标与图形的变化-旋转,菱形的性质,根据菱形的邻角互补对角线平分一组对角求出各角的度数,最后求出OB′与x轴负半轴的夹角是45°是解题的关键,也是本题的难点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
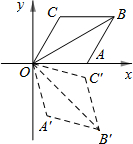 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=2
如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=2| 3 |
A、(3,
| ||||
B、(3,-
| ||||
C、(
| ||||
D、(
|
 (2013•兰州一模)如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y=
(2013•兰州一模)如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2),若反比例函数y= (2013•重庆)如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为
(2013•重庆)如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=
如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=