题目内容
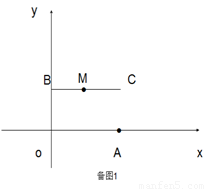
定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.根据上述定义,
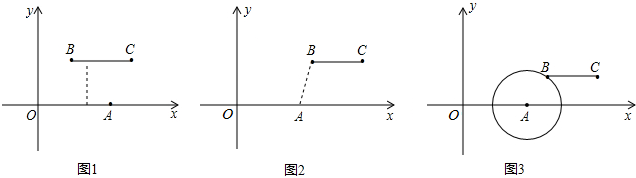
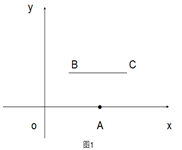
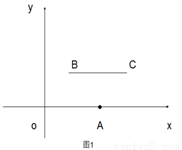
(1)当m=2,n=2时,如图1,线段BC与线段OA的距离是
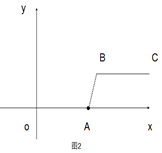
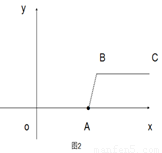
(2)当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为
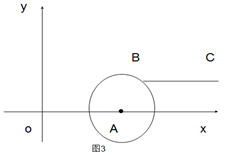
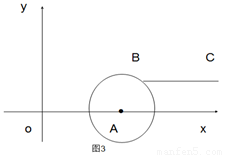
(3)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.

(1)当m=2,n=2时,如图1,线段BC与线段OA的距离是
2
2
,(2)当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为
| 5 |
| 5 |
(3)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
分析:(1)理解新定义,按照新定义的要求求出距离;
(2)按照新定义的要求,得出AB=
求出即可.
(3)如图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长.
(2)按照新定义的要求,得出AB=
| AN2+BN2 |
(3)如图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长.
解答: 解:(1)当m=2,n=2时,
解:(1)当m=2,n=2时,
如图1,线段BC与线段OA的距离等于平行线之间的距离,即为2;
故答案为:2;
(2)当m=5,n=2时,
B点坐标为(5,2),线段BC与线段OA的距离,即为线段AB的长,
如图2,过点B作BN⊥x轴于点N,则AN=1,BN=2,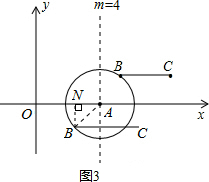
在Rt△ABN中,由勾股定理得:AB=
=
=
.
故答案为:
;
(3)如图3所示,当点B落在⊙A上时,m的取值范围为:2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长,
ON=m,AN=OA-ON=4-m,在Rt△ABN中,由勾股定理得:
故d=
=
=
(2≤m<4).
故d=
.
 解:(1)当m=2,n=2时,
解:(1)当m=2,n=2时,如图1,线段BC与线段OA的距离等于平行线之间的距离,即为2;
故答案为:2;
(2)当m=5,n=2时,
B点坐标为(5,2),线段BC与线段OA的距离,即为线段AB的长,
如图2,过点B作BN⊥x轴于点N,则AN=1,BN=2,

在Rt△ABN中,由勾股定理得:AB=
| AN2+BN2 |
| 12+22 |
| 5 |
故答案为:
| 5 |
(3)如图3所示,当点B落在⊙A上时,m的取值范围为:2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长,
ON=m,AN=OA-ON=4-m,在Rt△ABN中,由勾股定理得:
故d=
| 22-(4-m)2 |
| 4-16+8m-m2 |
| -m2+8m-12 |
故d=
|
点评:本题考查了圆的相关性质、点的坐标、勾股定理等重要知识点,根据新定义得出线段之间距离是解决本题的关键.

练习册系列答案
相关题目