题目内容
【题目】如图所示,已知△ABC中,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.
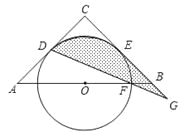
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和![]() 所围成的图形的面积(阴影部分).
所围成的图形的面积(阴影部分).
【答案】(1)∠BFG=∠BGF;理由见解析;(2)![]() -
-![]() .
.
【解析】
(1)连接OD,根据切线的性质可得出:OD∥GC,从而得出∠BGF=∠ODF.,由OD=OF得出∠ODF=∠OFD.然后利用等量代换可得∠BFG=∠BGF;(2)连接OE,根据阴影部分的面积=△DCG的面积-(正方形ODCE的面积 - 扇形ODE的面积)计算即可.
(1)∠BFG=∠BGF
连接OD,
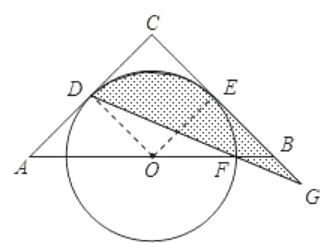
∵ OD=OF(⊙O的半径),
∴ ∠ODF=∠OFD.
∵ ⊙O与AC相切于点D,
∴ OD⊥AC
又∵ ∠C=90°,即GC⊥AC,
∴ OD∥GC,
∴ ∠BGF=∠ODF.
又∵ ∠BFG=∠OFD,
∴ ∠BFG=∠BGF.
(2)如图所示,连接OE,则ODCE为正方形且边长为3.
∵ ∠BFG=∠BGF,
∴ BG=BF=OB-OF=![]() ,
,
从而CG=CB+BG=![]()
∴ 阴影部分的面积=△DCG的面积-(正方形ODCE的面积 - 扇形ODE的面积)
![]()

练习册系列答案
相关题目