题目内容
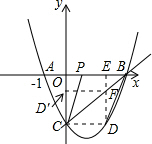
如图,抛物线y=ax2+bx-3a经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
(2)已知点D(m,-m-1)在第四象限的抛物线上,求点D关于直线BC对称的点D'的坐标.
(3)在(2)的条件下,连接BD,问在x轴上是否存在点P,使∠PCB=∠CBD?若存在,请求出P点的坐标;若不存在,请说明理由.

(1)求此抛物线的解析式;
(2)已知点D(m,-m-1)在第四象限的抛物线上,求点D关于直线BC对称的点D'的坐标.
(3)在(2)的条件下,连接BD,问在x轴上是否存在点P,使∠PCB=∠CBD?若存在,请求出P点的坐标;若不存在,请说明理由.

(1)将A(-1,0)、C(0,-3)代入抛物线y=ax2+bx-3a中,
得
,
解得
,
∴y=x2-2x-3;
(2)将点D(m,-m-1)代入y=x2-2x-3中,得
m2-2m-3=-m-1,
解得m=2或-1,
∵点D(m,-m-1)在第四象限,
∴D(2,-3),
∵直线BC解析式为y=x-3,
∴∠BCD=∠BCO=45°,CD′=CD=2,OD′=3-2=1,
∴点D关于直线BC对称的点D'(0,-1);
(3)存在.
过D点作DE⊥x轴,垂足为E,交直线BC于F点(如图),
∵∠PCB=∠CBD,
∴CP∥BD,
又∵CD∥x轴,四边形PCDB为平行四边形,
∴△OCP≌△EDB,
∴OP=BE=1,
设CP与BD相交于M点(m,3m-9),
易求BD解析式为:y=3x-9,
由BM=CM,得到关于m的方程,解方程后,得m=
;
于是,M点坐标为:M(
,-
);
于是CM解析式为:y=
x-3,
令CM方程中,y=0,则x=9,
所以,P点坐标为:P(9,0),
∴P(1,0),或(9,0).
得
|
解得
|
∴y=x2-2x-3;
(2)将点D(m,-m-1)代入y=x2-2x-3中,得
m2-2m-3=-m-1,
解得m=2或-1,
∵点D(m,-m-1)在第四象限,
∴D(2,-3),
∵直线BC解析式为y=x-3,
∴∠BCD=∠BCO=45°,CD′=CD=2,OD′=3-2=1,
∴点D关于直线BC对称的点D'(0,-1);
(3)存在.
过D点作DE⊥x轴,垂足为E,交直线BC于F点(如图),
∵∠PCB=∠CBD,
∴CP∥BD,
又∵CD∥x轴,四边形PCDB为平行四边形,

∴△OCP≌△EDB,
∴OP=BE=1,
设CP与BD相交于M点(m,3m-9),
易求BD解析式为:y=3x-9,
由BM=CM,得到关于m的方程,解方程后,得m=
| 9 |
| 4 |
于是,M点坐标为:M(
| 9 |
| 4 |
| 9 |
| 4 |
于是CM解析式为:y=
| 1 |
| 3 |
令CM方程中,y=0,则x=9,
所以,P点坐标为:P(9,0),
∴P(1,0),或(9,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 的高度是4米,离柱子OP的距离为1米.
的高度是4米,离柱子OP的距离为1米. 中央且距地面6m,建立如图所示的坐标系:
中央且距地面6m,建立如图所示的坐标系: