题目内容
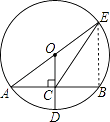
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连结BE,如图,
∵OD⊥AB,
∴AC=BC= ![]() AB=
AB= ![]() ×8=4,
×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,
解得:x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE= ![]() =
= ![]() =2
=2 ![]() ,
,
∴sin∠ECB= ![]() =
= ![]() =
= ![]() .
.
故选:B.
【考点精析】掌握垂径定理和圆周角定理是解答本题的根本,需要知道垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目






