题目内容
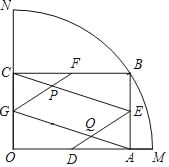
【题目】如图,扇形OMN的半径为1,圆心角为90°,点B是![]() 上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
(1)当点B移动到使AB:OA=![]() :3时,求
:3时,求![]() 的长;
的长;
(2)当点B移动到使四边形EPGQ为矩形时,求AM的长.
(3)连接PQ,试说明3PQ2+OA2是定值.
【答案】(1)证明见解析(2)当AM的长为(1﹣![]() )时,四边形EPGQ是矩形(3)定值
)时,四边形EPGQ是矩形(3)定值
【解析】
(1)先利用三角函数求出∠AOB=30°,再用弧长公式即可得出结论;
(2)易得△AED∽△BCE,根据相似三角形的对应边成比例与勾股定理,即可求得OA的长,即可得出结论;
(3)连接GE交PQ于O′,易得O′P=O′Q,O′G=O'E,然后过点P作OC的平行线分别交BC、GE于点B′、A′,由△PCF∽△PEG,根据相似三角形的对应边成比例与勾股定理,即可求得3PQ2+OA2的值.
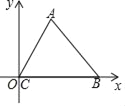
解:(1)证明:连接OB,如图①,
∵四边形OABC是矩形,
∴∠AOC=∠OAB=90°,
在Rt△AOB中,tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=30°,
∴![]() =
=![]() =
=![]() ;
;
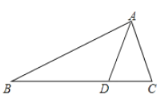
(2)如图②,∵EPGQ是矩形.
∴∠CED=90°
∴∠AED+∠CEB=90°.
又∵∠DAE=∠EBC=90°,
∴∠AED=∠BCE.
∴△AED∽△BCE,
∴![]() .
.
设OA=x,AB=y,则![]() =
=![]() ,
,
得y2=2x2,
又 OA2+AB2=OB2,
即x2+y2=12.
∴x2+2x2=1,
解得:x=![]() .
.
∴AM=OM﹣OA=1﹣![]()
当AM的长为(1﹣![]() )时,四边形EPGQ是矩形;
)时,四边形EPGQ是矩形;
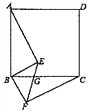
(3)如图③,连接GE交PQ于O′,
∵四边形EPGQ是平行四边形,
∴O′P=O′Q,O′G=O′E.
过点P作OC的平行线分别交BC、GE于点B′、A′.
由△PCF∽△PEG得,![]() =2,
=2,
∴PA′=![]() A′B′=
A′B′=![]() AB,GA′=
AB,GA′=![]() GE=
GE=![]() OA,
OA,
∴A′O′=![]() GE﹣GA′=
GE﹣GA′=![]() OA.
OA.
在Rt△PA′O′中,PO′2=PA′2+A′O′2,
即![]() =
=![]() +
+![]() ,
,
又 AB2+OA2=1,
∴3PQ2=AB2+![]() ,
,
∴OA2+3PQ2=OA2+(AB2+![]() )=
)=![]() 是定值.
是定值.