题目内容
已知矩形的对角线长为10cm，那么，顺次连接矩形四边中点所得的四边形周长为（ ）
| A、40cm | B、10cm | C、5cm | D、20cm |
分析：本题主要根据矩形的性质以及三角形中位线定理进行做题．
解答：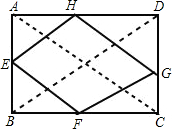
解：因为矩形的对角线相等，所以AC=BD=10cm，
∵E、F、G、H分别是AB、BC、CD、AD、的中点，
∴EH=GF=
BD=
×10=5cm，EF=GH=
AC=
×10=5cm，
故顺次连接矩形四边中点所得的四边形周长为EH+GF+EF+GH=5+5+5+5=20cm．
故选D．
解：因为矩形的对角线相等，所以AC=BD=10cm，∵E、F、G、H分别是AB、BC、CD、AD、的中点，
∴EH=GF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故顺次连接矩形四边中点所得的四边形周长为EH+GF+EF+GH=5+5+5+5=20cm．
故选D．
点评：本题比较简单，只要熟知矩形的对角线相等，三角形的中位线等于底边的一半即可．
练习册系列答案
相关题目