题目内容
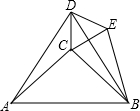如图，AC=BC，AC⊥BC于C，AB=AD=BD，CD=CE=DE．若AB=| 2 |
| A、1 | B、2 | C、3 | D、4 |
分析：根据等边三角形边长相等的性质，可以证明△ACD≌△BED，故AC=BE，已知AB，根据勾股定理即可求AC的长，即可解题．
解答：解：∵∠ADC+∠CDB=60°，∠CDB+∠BDE=60°，
∴∠ADC=∠BDE，
在△ACD和△BED中，
，
∴△ACD≌△BED，
∴AC=BE，
∵AC=BC，AB=
，
∴AC=BC=1，
∴BE=1．
故选A．
∴∠ADC=∠BDE，
在△ACD和△BED中，
|
∴△ACD≌△BED，
∴AC=BE，
∵AC=BC，AB=
| 2 |
∴AC=BC=1，
∴BE=1．
故选A．
点评：本题考查了勾股定理在直角三角形中的运用，全等三角形的证明和全等三角形对应边相等的性质，本题中求证△ACD≌△BED是解题的关键．
练习册系列答案
相关题目
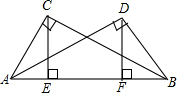如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB，垂足分别是E，F，那么，CE=DF吗？
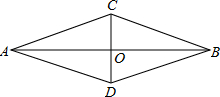已知，如图，AC=BC，AD=BD，下列结论中不正确的是（ ）
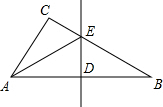如图，AC⊥BC，DE是AB的垂直平分线，∠CAE=30°，则∠B=
如图，AC⊥BC，AD=BD，为了使图中的△BCD是等边三角形，再增加一个条件可以是（ ）
已知如图：AC⊥BC，CD⊥AB，则点B到AC的距离是线段