题目内容
(2010•温州模拟)在平面直角坐标系xOy中(如图),已知二次函数y=x2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C.(1)确定此二次函数的解析式,并写出顶点C的坐标;
(2)将直线CB向上平移3个单位长度,求平移后直线l的解析式;
(3)在(2)的条件下,能否在直线上l找一点D,使得以点C、B、D、O为顶点的四边形是等腰梯形.若能,请求出点D的坐标;若不能,请说明理由.
【答案】分析:(1)分别把点A(0,3)和点B(3,0),代入二次函数y=x2+bx+c中得b=-4,c=3,求得二次函数的解析式;
(2)利于平移的性质,上加下减可知直线CB向上平移3个单位长度,求得平移后直线l的解析式;
(3)若四边形CBDO为等腰梯形,则只能BD=CO,且BC≠DO.设D(x,x),则利于两点间的距离公式可得D(1,1)或D(2,2),根据实际意义舍去D(1,1);若四边形CBOD为等腰梯形,则只能BO=CD,且BC≠DO,同理可得:D(-1,-1)或D(2,2),根据实际意义舍去D(-1,-1);从而求得点D的坐标.
解答:解:(1)把A(0,3)和B(3,0),代入y=x2+bx+c,
得: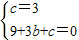 ,
,
解得: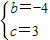 ,
,
所以,所求二次函数的解析式为:y=x2-4x+3
所以,顶点C的坐标为(2,-1)
(2)由待定系数法可求得直线BC的解析式为:y=x-3,
所以,直线l的解析式为:y=x
(3)能.
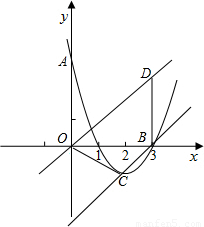 由直线l∥BC,即OD∥BC,可知:
由直线l∥BC,即OD∥BC,可知:
若四边形CBDO为等腰梯形,则只能BD=CO,且BC≠DO
∵点D为直线l:y=x上的一点
∴设D(x,x),则可得: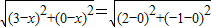 ①
①
解得:x1=1,x2=2经检验,x1=1,x2=2都是方程①的根
∴D(1,1)或D(2,2)
但当取D(1,1)时,四边形CBDO为平行四边形,不合题意,舍去
若四边形CBOD为等腰梯形,则只能BO=CD,且BC≠DO
同理可得:D(-1,-1)或D(2,2)
但当取D(-1,-1)时,四边形CBOD为平行四边形,不合题意,舍去
故所求的点D的坐标为(2,2).
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
(2)利于平移的性质,上加下减可知直线CB向上平移3个单位长度,求得平移后直线l的解析式;
(3)若四边形CBDO为等腰梯形,则只能BD=CO,且BC≠DO.设D(x,x),则利于两点间的距离公式可得D(1,1)或D(2,2),根据实际意义舍去D(1,1);若四边形CBOD为等腰梯形,则只能BO=CD,且BC≠DO,同理可得:D(-1,-1)或D(2,2),根据实际意义舍去D(-1,-1);从而求得点D的坐标.
解答:解:(1)把A(0,3)和B(3,0),代入y=x2+bx+c,
得:
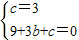 ,
,解得:
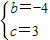 ,
,所以,所求二次函数的解析式为:y=x2-4x+3
所以,顶点C的坐标为(2,-1)
(2)由待定系数法可求得直线BC的解析式为:y=x-3,
所以,直线l的解析式为:y=x
(3)能.
 由直线l∥BC,即OD∥BC,可知:
由直线l∥BC,即OD∥BC,可知:若四边形CBDO为等腰梯形,则只能BD=CO,且BC≠DO
∵点D为直线l:y=x上的一点
∴设D(x,x),则可得:
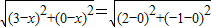 ①
①解得:x1=1,x2=2经检验,x1=1,x2=2都是方程①的根
∴D(1,1)或D(2,2)
但当取D(1,1)时,四边形CBDO为平行四边形,不合题意,舍去
若四边形CBOD为等腰梯形,则只能BO=CD,且BC≠DO
同理可得:D(-1,-1)或D(2,2)
但当取D(-1,-1)时,四边形CBOD为平行四边形,不合题意,舍去
故所求的点D的坐标为(2,2).
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
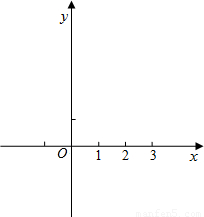
 +(2-
+(2-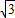 )-1-(
)-1-( )
) = .
= .